ellipse

ellipse

a closed conic section shaped like a flattened circle and formed by an inclined plane that does not cut the base of the cone. Standard equation x²/a² + y²/b² = 1, where 2a and 2b are the lengths of the major and minor axes. Area: πab

Collins Discovery Encyclopedia, 1st edition © HarperCollins Publishers 2005

ellipse

A closed curve that is a type of conic section with an eccentricity less than one. The longest line that can be drawn through the center of an ellipse is the major axis whereas the shortest line is the minor axis. The two axes are at right angles. There are two foci, which lie on the major axis and are symmetrically positioned on opposite sides of the center. The sum of the distances from the foci to a point moving round the ellipse is constant and equal to the length of the major axis. An orbiting body moves in an ellipse with the primary at one of the foci. See also Kepler's laws; orbit.

Collins Dictionary of Astronomy © Market House Books Ltd, 2006

Ellipse

A closed loop obtained by cutting a right circular cone by a plane.

Illustrated Dictionary of Architecture Copyright © 2012, 2002, 1998 by The McGraw-Hill Companies, Inc. All rights reserved

ellipse

[ə′lips]

(mathematics)

The locus of all points in the plane at which the sum of the distances from a fixed pair of points, the foci, is a given constant.

McGraw-Hill Dictionary of Scientific & Technical Terms, 6E, Copyright © 2003 by The McGraw-Hill Companies, Inc.

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Ellipse

 

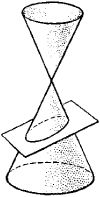
the intersection of a plane and one of the nappes of a circular conical surface (Figure 1).

Figure 1

An ellipse may also be defined as the locus of points M in the plane for which the sum of the distances from two fixed points F₁ and F₂ in the plane is constant; F₁ and F₂ are known as the foci of the ellipse. If a system of coordinates xOy is chosen as shown in Figure 2, then the equation of the ellipse assumes the form

Here, OF₁ = OF₂ = c, 2a = F₁M + F₂M, and .

Figure 2

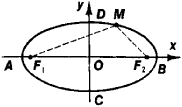
An ellipse is a quadratic curve. It is symmetric with respect to its axes AB and CD, and its center O is its center of symmetry. The line segments AB = 2a and CD = 2b are called the major and minor axes of the ellipse, respectively. The number e = cla < 1 is known as the eccentricity of the ellipse; if a = b, then e = 0 and the ellipse is a circle. The lines whose equations are x = –a/e and x = a/e are called the directrices of the ellipse; the ratio of the distance of a point of the ellipse from the nearest focus and the distance of the point from the nearest directrix is constant and equal to the eccentricity. The points A and B where the ellipse intersects its major axis are called its vertices. (See alsoCONIC SECTION.)

The Great Soviet Encyclopedia, 3rd Edition (1970-1979). © 2010 The Gale Group, Inc. All rights reserved.