Galilean transformations are given as shear motion on plane [2].
Galilean transformations in galilean space [G.sub.2]
Galilean transformations were examined widely in [2].
We redefine Galilean transformation by using quaternion operators.
f is a Galilean transformation, because the linear function f is a isometry.
Dual numbers and galilean transformation in [G.sub.2]
Dual Quaternions and galilean transformation in [G.sub.3]
Q = 1 + ai + bj is a Galilean transformation in [G.sub.3].
Thus the Q is a Galilean transformation. Furthermore, we can write g [member of] g(3) as g = [a.sub.1]i+[b.sub.1]j.
The point is that so long as the coordinate transformations map equal velocities into equal velocities (as is the case with linear transformations), then ff independence of the speed of the source holds for the light-speed in the resting frame (PCL), it automatically holds in the moving frame.(19) (This holds for the Galilean transformations and, say, sound propagation.) Thus, the only non-trivial element in PULC (given PLC) is precisely the condition that the (round-trip) light-speed in the moving frame is isotropic.
Reciprocity holds, of course, in classical kinematics, in the sense of being a consequence of the Galilean transformations. Clearly, however, this does not settle the issue when the relative velocity v between S and S|prime~ is large.
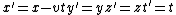where x, y, z and x′, y′, z′ are the space coordinates of a given particle, and v is the speed of one system relative to the other. See Frame of reference