Inflection, Point of
The point M of a plane curve is a point of inflection for the curve if the curve has a unique tangent at M and if in a sufficiently small neighborhood of M the curve is contained within one pair of the vertical angles formed by the tangent and normal (see Figure 1). The point (0, 0) of the curve y = x3 is an example of a point of inflection.
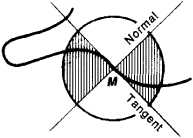
Suppose a curve is given by the equation y = f(x), where f(x) has the continuous second derivative f” (x). If the point with coordinates [x0, f (x0)] is a point of inflection, then f” (x) = 0; thus, a curve has zero curvature at a point of inflection. For a point to be a point of inflection it is necessary but not sufficient that f” (x) = 0. For example, that equality is satisfied by the curve y = x4 at the point (0, 0), although this point is not a point of inflection. A complete investigation of whether a given point of a curve is a point of inflection requires the use of higher order derivatives (if such derivatives exist) or other supplementary evidence.