Deviation

deviation

[‚dēv·ē′ā·shən]

(engineering)

The difference between the actual value of a controlled variable and the desired value corresponding to the set point.

(evolution)

Evolutionary differentiation involving interpolation of new stages in the ancestral pattern of morphogenesis.

(optics)

The angle between the incident ray on an object or optical system and the emergent ray, following reflection, refraction, or diffraction. Also known as angle of deviation.

(petroleum engineering)

During a drilling operation, the inclination of the borehole from the vertical.

(statistics)

The difference between any given number in a set and the mean average of those numbers.

McGraw-Hill Dictionary of Scientific & Technical Terms, 6E, Copyright © 2003 by The McGraw-Hill Companies, Inc.

deviation

i. The angular difference between a magnetic and a compass heading. It is a compass error caused by the compass magnet attempting to align with the aircraft's local magnetic field. The deviation error changes with the aircraft heading and the latitude. It is measured in degrees east (+) or west (−), depending on whether the north-seeking end of the compass needle lies to the east or west of magnetic north.
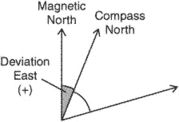
ii. The angle between the wind and the pressure gradient.
iii. In frequency modulation, the amount the carrier increases or decreases when modulated.
vi A departure from a current clearance, such as an off-course maneuver, to avoid bad weather or turbulence.
v A variation from set rules and regulations. Where specifically authorized in the regulation and requested by the pilot, ATC (air traffic control) may permit pilots to deviate from certain regulations.
vi. In flight, a sudden excursion from the normal flight path.
vii. The distance by which a weapon misses its target.

An Illustrated Dictionary of Aviation Copyright © 2005 by The McGraw-Hill Companies, Inc. All rights reserved

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Deviation

 

in artillery, an accidental phenomenon not allowed for in the laws of dispersion, by which shells (bullets) veer away from the mean trajectory expected under the given firing conditions. Causes of deviation may be the mechanical disruption of the movement of the shell in the bore (for example, separation of the shell from the rifling grooves) or in the air (for example, a defect in the stabilizer fins or other parts), as well as a chance sharp change in weather conditions during the flight of the shell.

---

Deviation

 

in biology, a variety of phylembryogenesis in which a change in the development of an organ arises in the middle stages of its formation and results in a change in the structure of the organ in the adult organism, compared with the same organ in its ancestors. For example, in the middle stages of development the epidermal part of the scale buds of reptiles undergoes keratinization, not ossification (as in sharks). The term “deviation” was introduced by the German scientist F. Müller (1864).

---

Deviation

 

the most common measure of dispersion, that is, deviation from the mean, in mathematical statistics and theory of probability. In the statistical sense, deviation

is the arithmetic mean of the squares of the deviations of the values Xi from their arithmetic mean

In the theory of probability the deviation (variance) of a random variable X is called the expected value E(X - m_x)² of the square of the deviation of X from its expected value m_x =E(X). The deviation of a random variable X is denoted by D(X) or by σ²). The square root of the deviation (that is, if the deviation is σ²) is called standard deviation.

For a random variable X with continuous probability distribution, characterized by probability density p(x), deviation is calculated by the formula

where

The following theorem has great significance in the theory of probability: the deviation of the sum of independent terms is equal to the sum of their deviations. No less important is Chebyshev’s inequality, which allows us to evaluate the probability of large deviations of the random variable X from its expected value.

REFERENCE

Gnedenko, B. V. Kurs teorii veroiatnostei, 5th ed. Moscow, 1969.

The Great Soviet Encyclopedia, 3rd Edition (1970-1979). © 2010 The Gale Group, Inc. All rights reserved.