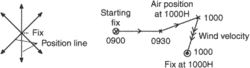
fix

fix

Nautical, etc the ascertaining of the navigational position, as of a ship, by radar, observation, etc.

Collins Discovery Encyclopedia, 1st edition © HarperCollins Publishers 2005

fix

[fiks]

(biology)

To kill, harden, or preserve a tissue, organ, or organism by immersion in dilute acids, alcohol, or solutions of coagulants.

(computer science)

A piece of coding that is inserted in a computer program to correct an error.

(navigation)

A position of a vessel or craft determined by its master, pilot, or navigator through the use of some or all of the equipments and techniques available.

McGraw-Hill Dictionary of Scientific & Technical Terms, 6E, Copyright © 2003 by The McGraw-Hill Companies, Inc.

FIX.

On drawings, abbr. for fixture.

McGraw-Hill Dictionary of Architecture and Construction. Copyright © 2003 by McGraw-Hill Companies, Inc.

fix

i. A geographical position determined by visual reference to the surface, by reference to one or more radio navigational aids, by celestial plotting, or by other navigational plotting, including obtaining it by intersecting two or more position lines. In navigation, a relatively accurate position determined without reference to any former position. It can be classified as visual, sonic, celestial, electronic, radio, hyperbolic, LORAN (long-range navigation), radar, etc., depending upon the means of establishing it.
ii. In photography, to render a photographic emulsion permanent by removing the unaffected light-sensitive material.

An Illustrated Dictionary of Aviation Copyright © 2005 by The McGraw-Hill Companies, Inc. All rights reserved

FIX

(networking)

Federal Information Exchange.

FIX

(business, protocol)

Financial Information eXchange.

fix

(3)

1. <mathematics> The fixed point combinator. Called Y in combinatory logic. Fix is a higher-order function which returns a fixed point of its argument (which is a function).

fix :: (a -> a) -> a fix f = f (fix f)

Which satisfies the equation

fix f = x such that f x = x.

Somewhat surprisingly, fix can be defined as the non-recursive lambda abstraction:

fix = \ h . (\ x . h (x x)) (\ x . h (x x))

Since this involves self-application, it has an infinite type. A function defined by

f x1 .. xN = E

can be expressed as

f = fix (\ f . \ x1 ... \ xN . E) = (\ f . \ x1 ... \xN . E) (fix (\ f . \ x1 ... \ xN . E)) = let f = (fix (\ f . \ x1 ... \ xN . E)) in \ x1 ... \xN . E

If f does not occur free in E (i.e. it is not recursive) then this reduces to simply

f = \ x1 ... \ xN . E

In the case where N = 0 and f is free in E, this defines an infinite data object, e.g.

ones = fix (\ ones . 1 : ones) = (\ ones . 1 : ones) (fix (\ ones . 1 : ones)) = 1 : (fix (\ ones . 1 : ones)) = 1 : 1 : ...

Fix f is also sometimes written as mu f where mu is the Greek letter or alternatively, if f = \ x . E, written as mu x . E.

Compare quine.

This article is provided by FOLDOC - Free Online Dictionary of Computing (foldoc.org)