function
function
the consequence for a social system of a social occurrence, where this occurrence is regarded as making an essential contribution to the working and maintenance of this system. See FUNCTIONALISM, STRUCTURAL-FUNCTIONALISM, PARSONS, MERTON, FUNCTIONAL(IST) EXPLANATION, FUNCTIONAL PREREQUISITES, POSTULATE OF FUNCTIONAL INDISPENSABILITY.A distinction is also made between consequences of social action that are intended and recognized by the actors involved, and consequences that are unintended and unrecognized by the actors involved. See MANIFEST AND LATENT FUNCTIONS, MERTON, INTENDED AND UNINTENDED CONSEQUENCES OF SOCIAL ACTION.
function
[′fəŋk·shən]function
(mathematics)function
(2)function
(3)See also image, inverse, partial function.
function
(programming)A procedure is a function which returns no value but has only side-effects. The C language, for example, has no procedures, only functions. ANSI C even defines a type, void, for the result of a function that has no result.
function
In programming, a self-contained software routine that performs a task. Functions can do a large amount of processing or as little as adding two numbers and deriving a result. Values are passed to the function, and values may be returned. Or, the function may just perform the operation and not return a resulting value. The concept of a function within a program is that, once written, it can be used over and over again without the programmer having to duplicate the same lines of code in the program each time that same processing is desired.Standard and Programmer-Defined
Programming languages provide a set of standard functions as well as allow programmers to define their own functions. For example, the C and C++ programming languages are built entirely of functions and always contain a "main" function.
The Application Programming Interface (API)
Functions in one program can also be called for by other programs and shared. For example, operating systems can contain more than a thousand functions to display data, print, read and write disks and perform myriad tasks. Programmers write their applications to interact with the OS using these functions. This list of functions is called the "application programming interface" (API).
Function Calls
Functions are activated by placing a "function call" statement in the program. The function call often includes values (parameters) that are passed to the function. When called, the function performs the operation and returns control to the instruction following the call. The function may return a value or not. Writing a program in a language such as C/C++ involves calling language functions, one's own functions and operating system functions (APIs). There is a whole lot of function calling. See function prototype, API and interface.
A Function Call Example: Open and Read
The example below shows two very simplified API functions to open and read a file.
The OPEN function is called to read the file "budget.txt," and the function returns a value in the variable HANDLE. If the file was opened successfully, HANDLE might contain a positive number, but if not, a negative one. The value in HANDLE is then passed to the READ function to read so many bytes (LENGTH) of the file into a memory area called INPUTBUFFER. The OPEN function returns the number of bytes read in the SIZE variable.
handle = open("budget.txt");
size = read(handle, InputBuffer, length);
Function
in linguistics, the ability of a given linguistic form to fulfill a certain function; the term is used to denote the meaning or purpose of a linguistic form. Function refers to the dependence or relationship among the units of a language as these units are revealed at all levels of the language’s system.
In order to determine the function of a linguistic unit it is necessary to determine the unit’s role in a given language or linguistic system. For example, it is possible to isolate from a sentence its communicative function, which is to supply information about something, and its nominative function, which is to name the subject about which the information is supplied. Each linguistic unit exists solely because it serves a specific aim that is distinct from the aim of another linguistic unit; that is, each linguistic unit fulfills a specific function. The many different functions of linguistic units include functions of identification and of delimitation and differentiation. In the functions of delimitation and differentiation, the linguistic units themselves are distinguished. For exam-pie, a phoneme serves to differentiate among different words and morphemes or to indicate the boundaries between them.
Functions are analyzed when the units of a language are described and also when the language itself is described as a system. Among the main functions of a language are the communicative, cognitive, reflective, and performatory functions. The phatic function is the use of speech to establish personal contact rather than to communicate information. The nominative function is the use of language to name objects and concrete phenomena. Other functions of a language are the expressive and appellative functions.
The functions of a language also include functions relating to levels of language, that is, phonological, morphological, and grammatical functions. From the functional point of view, a linguistic system is a complex structure that may be differentiated according to its means of expression (written or spoken language), its social role (literary language, socially differentiated dialects, or slang), or its aesthetic orientation (poetic language). A linguistic system may also be differentiated in terms of concrete objectives of communication, and to that end makes use of specialized systems of terminology.
E. S. KUBRIAKOVA
Function
a fundamental concept of mathematics expressing the dependence of one variable on another.
If the variables x and y are connected so that to every value of x there corresponds a definite value of y, then y is said to be a (single-valued) function of x. Frequently x is referred to as the independent variable, and y as the dependent variable. Common ways of denoting this type of connection between x and y are y = f(x)andy = F(x). If the relation between x and y is such that to some values of x there correspond many (possibly even infinitely many) values of y, then y is said to be a multivalued function of x.
A function y = f(x) is said to be defined if we are given a set A of values taken on by x (the domain of the function), a set B of values taken on by y (the range of the function), and a rule that associates to values of x in A values of y in B. The simplest domains of functions are the real line, a closed interval a ≤ x ≤ b, and an open interval a < × < b.
The most frequent way of assigning to values of x the corresponding values of y is to give a formula that indicates what operations must be applied to x to obtain y. Examples of such formulas are y = x2 and y = 1/(1 + x2). In addition to the four arithmetic operations, the list of computing (or analytic) operations usually includes the operation of passing to the limit (that is, the operation that associates to a sequence of numbers a1, a2, a3. . . . its limit lim an whenever the limit exists), although there are no general methods for carrying out the operation. In 1905, H. Lebesgue defined an analytically representable function as a function whose values are obtained from the values of x by means of the four arithmetic operations and the operation of passing to the limit. All the functions known as elementary functions, such as sin x, cos x, ax, 
, log x, and arc tan x, are analytically representable. For example,
In 1885, K. Weierstrass proved the analytic representability of an arbitrary continuous function. Specifically, he proved that every function continuous on a closed interval is the uniform limit of a sequence of polynomials of the form
c0 + c1x + c2x2 + . . . cnxn
In addition to the analytic method there are other methods of defining functions. For example, in trigonometry cos x is defined as the projection of a unit vector on an axis that forms with the vector an angle of x radians, and in algebra is defined as the number whose square is ψx. The possibility of representing these functions by means of analytic formulas can be established only through deep study of the functions. In this connection the Dirichlet function ɸ(x) may be mentioned. It equals 1 if x is rational and 0 if x is irrational. The Dirichlet function was first introduced in this “formula-free” manner but was subsequently shown to be given analytically by the formula
It is important to note that there exist functions that cannot be represented, in the sense given above, by any analytic formula. Examples of such functions are functions that are not Lebesgue measurable.
A concept close to that of a function defined by a single formula is that of a function defined by different formulas in different parts of its domain of definition. One relevant example is the function f(x) = x for x ≤ 1 and f(x) = x2 for x > 1. Another is the Dirichlet function ψ(x) as defined above in a “formula-free” manner.
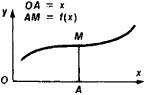
Sometimes a function y = f(x) is given by its graph, that is, the set of points (x, y) in the plane such that x is in the domain of definition of the function and y = f(x). In applications it often suffices for the graph of a function to be drawn in the plane (see Figure 1), the functional values being obtained directly from the drawing. For example, the upper layers of the atmosphere can be studied by means of balloons equipped with recording instruments that yield directly curves of variation of temperature and pressure.
For a mathematically correct definition of a function it is not enough to draw the function’s graph, since such a procedure is intrinsically inaccurate. A graphic definition of a function thus requires giving an exact geometric construction of the graph. In most cases the construction is given by means of an equation— that is, we are brought back to the analytic definition of a function. There do exist, however, purely geometric ways of constructing certain graphs; for example, a straight line is determined by giving the coordinates of two of its points.
In engineering and in the sciences it often happens that the variables x and y are known to be functionally related but the relation itself is unknown. A more or less extensive table of pairs of numbers “belonging” to the function can be obtained by carrying out a number of experiments in each of which a value of x and the corresponding value of y are measured. On many occasions the finding of an analytic formula for a function by means of such a table has constituted an important scientific discovery. An example is the discovery, by R. Boyle and E. Mariotte, of the formula pv = C connecting the pressure and volume of a gas sample. From a purely mathematical point of view, the defining of a function by means of a table of number pairs is entirely correct provided we take as the domain of definition of the function the set of first entries of the pairs in the table and assume that in each case the second entry is strictly accurate.
Functions of more than one variable also play an important role in mathematics and its applications. Suppose, for example, that to every set of values of the three variables x, y, and z there corresponds a definite value of a fourth variable u. We then say that u is a (single-valued) function of the variables x, y, and z, and we write u = f(x, y, z). The formulas u = x + 2y and u = (x + y2) sin z provide examples of the analytic definition of functions of two and three variables, respectively. There are analogous definitions of multivalued functions of more than one variable. A function z = f(x, y) of two variables may also be defined by means of its graph, that is, the set of triples (x, y, z) in three-dimensional space with (x, y) in the domain of definition of the function and z = f(x, y). In simple cases such a graph is some surface.
The development of mathematics in the 19th and 20th centuries led to further generalizations of the function concept. First, complex, rather than real, numbers were admitted as values of the variables; later, variable mathematical objects of an arbitrary nature were considered. For example, if to every circle x in the plane we associate its area y, then y is a function of x, where x is a geometric figure and not a number. Similarly, if to every sphere x in three-dimensional space we associate its center y, then neither x nor y is a number.
A general definition of a single-valued function follows. Let A = {x} and B = {y} be two nonempty sets of arbitrary objects and let M be the set of ordered pairs (x, y), x ∈ A, y ∈ B, such that every x ∈ A belongs to exactly one pair in M. Then M defines a function y = f(x) on A whose value at x0 ∈ A is the second element y0 ∈ B of the pair in M with first element x0.
This generalized definition of function eliminates the distinction between functions of one and many variables. For example, a function of three numerical variables x, y, and z may be regarded as a function of a single variable, namely, the point (x, y, z) in three-dimensional space. The definition also accommodates such generalizations of the function concept as functional and operator.
Like all mathematical concepts, the concept of a function was the result of a long evolutionary process. P. Fermât, for example, wrote in his Introduction to Plane and Solid Loci: “Whenever in a final equation two unknown quantities are found, we have a locus.” In essence, Fermât is speaking here of a functional dependence and its graphical representation, since for him “locus” means curve. The study of curves through their equations in R. Descartes’s Geometry (1637) also points to a clear notion of the mutual dependence of two variable quantities. In his Lectures on Geometry (1670), I. Barrow established by a geometric argument that differentiation and integration (of course, Barrow did not use these terms) are mutually inverse operations. This achievement indicates a very precise understanding of the concept of function. A geometric and mechanical form of the concept of function is also found in the work of I. Newton. The term “function” was first used in 1692 by G. von Leibniz. His usage of the term, however, was somewhat different from the modern usage. By a function Leibniz meant various intervals associated with a curve—for example, the abscissas of the curve’s points. In G. de L’Hôpital’s Infinitesimal Analysis (1696), which was the first published textbook on differential calculus, we do not encounter the term “function.”
In 1718, Johann Bernoulli became the first to define the function concept in a manner similar to that of today: “A function is a quantity formed of a variable and a constant.” This imprecise formulation suggests the idea of a function defined by an analytic formula. The same idea is found in L. Euler’s definition in his Introduction to the Analysis of Infinitesimals (1748): “A function of a variable quantity is an analytic expression formed, in any manner whatever, of the variable quantity and of numbers or constant quantities.” Euler also entertained the modern view of a function, which does not involve analytic expressions. Thus, in his Differential Calculus (1755), Euler states that “if certain quantities depend on others in such a way that the former vary with the latter, then the former are said to be functions of the latter.”
Nevertheless, a sufficiently sharp distinction was not made in the 18th century between a function and its analytic representation. This fact is reflected in Euler’s critique of D. Bernoulli’s solution (1753) of the problem of the vibrating string. Bernoulli’s solution was based on the assumption that every function was representable by a trigonometric series. Euler pointed out that this assertion implied the existence of an analytic expression for every function. He argued that it was possible for a function not to have an analytic representation; an example would be a function given by a graph “drawn freehand.” This critique carries weight even today. (Bernoulli, of course, considered only continuous functions, and such functions always admit of analytic representations; nevertheless, continuous functions need not admit of representations by trigonometric series.) Some of Euler’s other arguments, however, were false. For example, he thought that if a function is representable by a trigonometric series then the series is the function’s only analytic representation; in actuality, the function may be a “mixed” function represented by different formulas on different intervals. We now know that no contradiction is involved here, but in Euler’s time it was unthinkable that two analytic expressions could agree on part of an interval but not on all of it.
Such incorrect views hampered the development of the theory of trigonometric series. The essentially correct ideas of D. Bernoulli did not undergo further development until the work of J. Fourier (1822) and P. Dirichlet (1829).
In the 19th century the function concept came to be more frequently defined without any reference to analytic representability. Thus, in his treatise on the calculus (1810) the French mathematician S. Lacroix wrote: “Every quantity whose value depends on one or several others is called a function of the latter.” Fourier’s Analytical Theory of Heat (1822) contains the following sentence: “A function fx is an entirely arbitrary function, that is, it is a succession of given values that may or may not be subject to a general law and that correspond to all values x contained between 0 and some quantity X.” N. I. Lobachevskii’s definition in “On the Convergence of Trigonometric Series” (1834) is close to the modern one: “The general concept demands that we call a function of A: a number determined for every x and varying together with x. The value of a function may be given by an analytic expression, or condition, that permits the testing of all numbers and the selection of one of them. Finally, a dependence may exist that remains unknown.” Later in the same work he wrote: “A broad view of the theory admits the existence of a dependence only in the sense that we regard linked numbers as being given simultaneously.” Thus, the modern definition of function—that is, a definition free of any reference to analytic representability—appeared a number of times before being stated by Dirichlet, its presumed discoverer, in 1837.
In conclusion, an important discovery due to D. E. Men’shov should be mentioned: every finite Lebesgue measurable function defined on a closed interval can be expanded in a trigonometric series that converges almost everywhere. Since the functions usually encountered are measurable, it is essentially correct to say that, except on a set of measure zero, every function admits of an analytic representation.
REFERENCES
Il’in, V. A., and E. G. Pozniak. Osnovy matematicheskogo analiza, 3rd ed., parts 1–2. Moscow, 1971–73.Kudriavtsev, L. D. Matematkheskii analiz, 2nd ed., vols. 1–2. Moscow, 1973.
Nikol’skii, S. M. Kurs matematicheskogo analiza, 2nd ed., vols. 1–2. Moscow, 1975.
I. P. NATANSON
Function
in philosophy, a relationship between two objects (or within a group of objects) such that a change in one results in a change in the other. Functions may be considered in terms of (1) the consequences—favorable, unfavorable (or dysfunctional), or neutral (that is, afunctional)—of change in one parameter affecting other parameters of an object, in which case we speak of functionality, or (2) the interrelated functioning of the individual parts within a given whole.
The scientific concept of function was introduced by G. von Leibniz. Subsequently regarded as one of the fundamental categories in philosophy, functions attracted increasing interest with the adoption of functional methods of research in various scientific disciplines. The functional approach was most fully developed by E. Cassirer in his theory of concepts, or “functions.” This attempt to construct a theory of knowledge on the basis of the functional approach had a definite influence on the philosophical concept of function. Current research deals with the validity, admissibility, and demonstrability of functional statements and explanations that are commonly used in the biological and social sciences, especially in connection with the study of goaldirected systems.
REFERENCES
Iudin, B. G. “Sistemnye predstavleniia v funktsional’nom podkhode.” In the collection Sistemnye issledovaniia: Ezhegodnik 1973. Moscow, 1973. Pages 108–26.Frege, G. Funktion und Begriff. Jena, 1891.
Wright, L. “Functions.” Philosophical Review, vol. 82, April 1973, pp. 139–68.
Cummins, R. “Functional Analysis.” The Journal of Philosophy, 1975, vol. 72, no. 20.
In Russian translation:
Cassirer, E. Poznanie i deistvitel’nost’: Poniatie o substantsii i poniatie ofunktsii. St. Petersburg, 1912.
See also references under SYSTEM and SYSTEMS APPROACH.
(2) The dependent relationship found to exist between the various components of a single social process wherein changes in one part of the system result from changes in another part—for example, changes in the relative size of urban and rural populations as a function of industrial development.
The Marxist approach to the study of functions is based on the class analysis of the institutions themselves as well as of the corresponding needs and interests.
REFERENCES
See references under SYSTEM and STRUCTURAL-FUNCTIONAL ANALYSIS.A. G. ZDRAVOMYSLOV
Function
an action performed by human beings, animals, and plants to maintain life processes and to make possible adaptation to environmental conditions. Physiologists study functions at the molecular, cellular, tissular, organic, and systemic levels, as well as those at the level of the integral organism. The systemic functions of animals include respiration, cardiovascular activity, digestion, vision, hearing, and equilibrium. Since all functions are based on the continuous process of metabolism, they are studied in order to elucidate the physical, chemical, and structural changes that take place in the body (in the system of organs or in individual organs and tissues). Of considerable importance in this respect is research in developmental biology, a field concerned with the processes and propelling forces of individual development (ontogeny).
The comparative historical method introduced into physiology by I. M. Sechenov, I. P. Pavlov, and N. E. Vvedenskii played a major part in the comprehensive study of functions. L. A. Orbeli and his school pioneered the study of the physiological, biochemical, and structural bases of the evolution of functions (evolutionary physiology). Their work influenced the study of functional changes induced by various factors of natural or artifical origin, for example, changes in climatic conditions, motor activity, composition and properties of food, insufficiency or excess of atmospheric oxygen, and weightlessness, as well as the study of adaptation to environmental conditions.
The study of the evolution of functions and, especially, the adaptability of functions to the environment is closely associated with the investigation of the mechanisms that regulate functions (seeHUMORAL REGULATION, HORMONAL REGULATION, and NEURO-HUMORAL REGULATION). The views of K. M. Bykov and his school on the relationship between the cerebral cortex and the internal organs marked an important stage in the study of functions (seeCORTICOVISCERAL RELATIONS). Development of the concept of corticovisceral relations led to an explanation of the regulation of the visceral systems of the body based on the idea that their activity is a distinctive form of behavior. Inasmuch as the functions of the visceral systems, like the behavior of the organism as a whole, are always adaptive, they develop in the fairly strict sequence of the individual reactions that constitute them and, moreover, possess the capacity to “learn,” that is, become perfected. The objective of research in this field is to elucidate the mechanisms and patterns of regulation of functions in order to make possible intervention to normalize the body’s vital activities in the event of abnormal or extreme conditions.
V. N. CHERNIGOVSKII and K. A. LANGE