star
star
A luminous gaseous body that generates energy by means of nuclear fusion reactions in its core. Below a certain mass (0.08 solar masses), the central pressures and temperatures in a body are insufficient to trigger fusion reactions; all stars must therefore exceed this mass limit. Stars of progressively higher mass are less and less common; the highest reliably determined values are about 60 to 120 solar masses, but there may be a very few more massive stars (see stellar mass).Although there is only a relatively narrow range in normal stellar masses, it is the mass of a star that determines its other properties – luminosity, temperature, size – and the way in which it evolves. These quantities are related to the mass by the equations of stellar structure. Other stellar parameters show a far greater range than stellar mass: for example, the luminosity of a star is proportional to roughly the fourth power of its mass for a solar-type star, and the cube power of its mass for a massive star (see mass-luminosity relation); stars therefore show a range in luminosity of some 1010. A star's lifetime also depends on its mass: low-mass stars live considerably longer than high-mass ones.
All stars are composed predominantly of hydrogen and helium; this was first proposed in 1925 by Cecilia Payne-Gaposchkin and confirmed in 1929 by H.N. Russell. The proportions of the chemical elements in the Sun are not significantly different from those in most other stars. This general composition by mass is 70% hydrogen, 28% helium, with the remaining elements – known in astronomy as metals or heavy elements – making up just 2%; by numbers of atoms it is 90.8% hydrogen, 9.1% helium, 0.1% metals.
The characteristics of a star can be determined only when its distance is known. The method of distance determination depends on the distance itself: the shortest distances are found directly by measuring a star's annual parallax; greater distances require indirect methods. The nearest star, Proxima Centauri, is 1.3 parsecs away. The stars in our immediate locality are found in the main to be young stars occupying the outer parts of the disk of our Galaxy, rotating around the galactic center. Many still remain in open clusters, and over 50% of all the stars we observe are binary stars or multiple stars.
See also magnitude; population I, population II; spectral types; star formation; stellar evolution; variable star.
Star
(religion, spiritualism, and occult)A star is a self-luminous celestial body. Although not usually thought of in these terms, the Sun is also a star. Self-luminosity distinguishes stars from planets, which shine by virtue of reflected light. The ancients did not make this distinction but instead referred to the planets as wandering (the etymological meaning of the word planet) stars, and to the stars proper as fixed stars.
What does it mean when you dream about a star?
Stars are prominent in the mythologies from cultures the world over. In a dream they can symbolize anything from heaven to the mysteries of the universe to luck (“born under a lucky star”) to fame and fortune.
star
[stär]STAR
[stär]star
Star
The Xerox workstation that officially introduced the graphical user interface and desktop metaphor in 1981. It was the inspiration for Xerox's subsequent computers and for Apple's Lisa and Macintosh. All graphical user interfaces owe their roots to the Star. See Alto.| The Star User Interface |
|---|
| If the graphical interface and simulated desktop in this picture seem amazingly similar to the Macintosh and Windows, there is a reason why. That is where they both came from. (Image courtesy of Palo Alto Research Center.) |
Star
(dreams)Star
a self-luminous celestial body that consists of incandescent gases and is similar in nature to the sun. The sun seems incomparably larger than the stars only because of its proximity to the earth: light travels from the sun to the earth in 8⅓ min, while from the nearest star, α Centauri, in four years and three months. Owing to their great distances from the earth, stars are visible as points not as disks, even in telescopes (in contrast to planets). About 5,000 stars are visible to the naked eye in both celestial hemispheres on a moonless night. Billions of stars are visible in powerful telescopes.
General information. Short history of the study of stars. The study of the stars grew out of efforts to meet specific needs of society (necessity for orientation during voyages, establishment of calendars, determination of exact time). As far back as remote antiquity the stellar sky had been divided into constellations. For a long time the stars were considered as fixed points in relation to which the motions of planets and comets were observed. From the time of Aristotle (fourth century B.C.) it was believed for many centuries that the stellar sky was an eternal and immutable crystal sphere, beyond the boundaries of which was the abode of the gods. At the end of the 16th century the Italian astronomer Giordano Bruno taught that the stars were distant bodies similar to our sun. The first variable star was discovered in 1596 (by the German astronomer D. Fabricius) and the first double star, in 1650 (by the Italian scientist G. Riccioli). In 1718 the English astronomer E. Halley discovered the proper motions of three stars. In the second half of the 18th century the Russian scientist M. V. Lomonosov, the German scientist I. Kant, and the British astronomers T. Wright and W. Herschel, among others, expressed correct ideas concerning the stellar system to which the sun belongs. Between 1835 and 1839 the Russian astronomer V. la. Struve, the German astronomer F. Bessel, and the British astronomer T. Henderson determined for the first time the distances to three nearby stars. In the 1860’s the spectroscope was used for the study of the stars, and photographs began to be used in the 1880’s. In 1900 the Russian astronomer A. A. Belopol’skii experimentally demonstrated the validity of Doppler’s principle for optical phenomena, on the basis of which it is possible to determine the velocity of a celestial object along the line of sight according to the shift in the lines of its spectrum. The accumulation of observations and the development of physics have broadened our knowledge of stars.
In the early 20th century, particularly after 1920, revolutionary ideas emerged in science about the stars. Stars began to be viewed as physical bodies; their structure, the equilibrium conditions of their constituents, and their sources of energy began to be studied. The emergence of these ideas was connected with the successes of atomic physics, which led to a quantitative theory of stellar spectra, and with the achievements of nuclear physics, which made possible analogous calculations of the energy sources and of the internal structures of stars (the most important results were obtained by the German scientists R. Emden, K. Schwarzschild, and H. Bethe; the British scientists A. Eddington, E. A. Milne, and J. Jeans; the American scientists H. Russell and R. F. Christy; and the Soviet scientist S. A. Zhevakin). In the mid-20th century the study of stars acquired still greater depth with the expansion of observational resources and the use of computers (the American scientists M. Schwarzschild and A. Sandage, the British scientist F. Hoyle, the Japanese scientist C. Hayashi). Great success was also achieved in studies of the transport of energy in stellar photospheres (the Soviet scientists E. R. Mustel’ and V. V. Sobolev and the American scientist S. Chandrasekhar) and in investigations of the structure and dynamics of stellar systems (the Dutch scientist J. Oort, the Soviet scientists P. P. Parenago and B. V. Kukarkin).
Stellar parameters. The fundamental characteristics of a star are its mass, radius (excluding the outer transparent layers), and luminosity (total amount of radiated energy). These quantities are often expressed as fractions of the sun’s mass, radius, and luminosity. The following parameters derived from the fundamental parameters are also used: the effective temperature; the spectral class, which characterizes the degree of ionization and excitation of the atoms in the stellar atmosphere; the absolute stellar magnitude (that is, the magnitude that the star would have at the standard distance of 10 parsecs); and the color index (the difference in magnitudes determined in two different spectral regions).
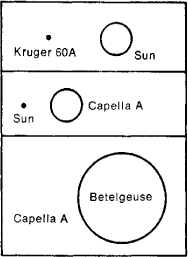
The stellar population is extremely diverse. Certain stars are millions of times larger (in volume) and brighter than the sun (giant stars). At the same time there are many stars that are significantly surpassed by the sun in size and the amount of energy they radiate (dwarfs) (see Figure 1). The luminosities of stars are also diverse. Thus, the luminosity of the star S Doradus is 400,000 times greater than that of the sun. Stars can be diffuse or extremely dense. The average density of a number of giants is hundreds of thousands of times less than the density of water, while the average density of the so-called white dwarfs is, on the contrary, hundreds of thousands of times greater. Stars vary less in mass.
The brightness of certain types of stars changes periodically; such stars are called variable stars. Immense changes, accompanied by sudden increases in brightness, occur in novas. In these, a small star, a dwarf, increases for several days. A gaseous shell separates out. This shell continues to expand and, as it expands, dissipates in space. The star then contracts again to a small size. Still greater variations occur during the outbursts of supernovas.
The study of the spectra of stars permits the determination of the chemical composition of their atmospheres. Stars, like the sun, consist of the same chemical elements found on the earth. Hydrogen (about 70 percent by weight) and helium (about 25 percent) predominate in stars; the remaining elements, among which the most abundant are oxygen, nitrogen, iron, carbon, and neon, are found in almost exactly the same ratios as on the earth. As yet, only the outer layers of stars are accessible to observation. However, the correlation of the data from direct observations with conclusions resulting from the general laws of physics have made it possible to construct a theory of the internal structure of stars and the sources of stellar energy.
From all indications, the sun is a typical star. There is every reason to believe that many stars have a planetary system like that of the sun. Because of their remoteness, it is still impossible to directly observe such satellites of the stars even with the most powerful telescopes. Subtle methods of investigation, accurate observations over dozens of years, and complex calculations are necessary for their detection. In 1938 the Swedish astronomer E. Holmberg began to suspect and later the Soviet astronomer A. N. Deich and others established the existence of invisible satellites belonging to the star 61 Cygni and other stars near the sun. Our planetary system is thus not an exceptional phenomenon. Life probably also exists on many planets circling other stars, and the earth does not represent an exception in this respect.
Stars are often located in pairs revolving around a common center of mass; such stars are called binary stars. Triple stars and multiple stellar systems are also encountered.
The arrangement of the stars with respect to each other changes slowly with time because of their motion in the galaxy. Stars form huge stellar systems in space—galaxies. The Milky Way Galaxy (to which the sun belongs) is composed of more than 100 billion stars. The study of its structure shows that many stars are grouped into star clusters, stellar associations, and other formations.
There are two complementary approaches in the study of stars. Stellar astronomy, which views stars as objects characterized by certain properties, studies the motion of stars, their distribution in our galaxy and in clusters, and their different statistical regularities. The physical processes occurring in stars and their radiation, structure, and evolution are studied in astrophysics.
Stellar masses. Masses can be directly determined only for binary stars on the basis of the study of their orbits. For spectroscopic binaries, measuring the Doppler shift of the spectral lines makes it possible to determine the period of revolution of the components and the projection of the maximum velocity of each component on the line of sight. Similar measurements may be carried out for certain visual binaries. The data are sufficient for the calculation of the ratios of the masses of the components. The absolute values of the masses can be determined if the system is at the same time an eclipsing binary, that is, if its orbit is seen edgewise and the components alternately eclipse each other. The study of the masses of binary stars reveals the existence of a statistical relation between the masses and luminosities of main-sequence stars. This relation, which is also valid for single stars, permits an indirect estimate of the masses of stars by determining their luminosities.
Stellar luminosities and distances. The primary method of determining the distances to stars consists of measuring their apparent displacement against the background of more distant stars as the earth revolves around the sun. The distance itself is computed according to the displacement (parallax), whose magnitude is inversely proportional to the distance. However, this method of measurement is applicable only to the nearest stars.
If the distance to a star and its apparent magnitude m are known, the absolute magnitude M can be found from the formula
M = m + 5 − 5 log r
where r is the distance to the star expressed in parsecs. Having determined the average absolute magnitudes for stars of different spectral classes and having compared them with the apparent magnitudes of specific stars of these same classes, one may also determine the distances to remote stars, for which the parallactic displacements are imperceptible (so-called spectroscopic parallaxes). Absolute magnitudes of certain types of variable stars (for example, cepheids) can be determined from the period of their luminosity, and this also permits the determination of their distances.
Distances are also estimated from the systematic components of the radial velocities and proper motions of the stars caused by peculiarities of the rotation of the galaxy and the motion of the sun (together with the earth) in space and thus depending on the distance of the star. In order to eliminate the effects of the proper velocities of individual stars, distances to large groups of stars are determined at the same time (statistical or group parallaxes).
The brightest stars are given in Table 1 and the nearest stars, in Table 2.
Stellar temperatures and spectral classes. The distribution of energy in the spectra of incandescent bodies is not uniform. The maximum in radiation intensity falls at different wavelengths at different temperatures, and the color of the overall radiation changes. Investigation of these effects in stars, the study of the energy distribution in stellar spectra, and measurements of the color indexes allow the temperatures of stars to be determined. Stellar temperatures are also determined according to the relative intensities of certain lines in their spectra, permitting the spectral class of the stars to be ascertained. Spectral classes of stars depend on temperature and are designated by the letters O, B, A, F, G, K, and M in order of decreasing temperature. In addition, a secondary sequence of carbon stars C (formerly designated R and N) branches out from class G and a secondary branch S, from class K. The hotter stars—nuclei of planetary nebulas (class P) and Wolf-Rayet stars with broad emission lines in the spectrum (class W)—are separated from class O. If the mechanism of formation of spectral lines is known, then the temperature can be computed according to the spectral class if the acceleration of gravity on the star’s surface is known. This is related to the average density of its photosphere and, consequently, to the dimensions of the star (the density may be evaluated from
| Table 1. The brightest stars | ||||||||
|---|---|---|---|---|---|---|---|---|
| Name | Apparent magnitude (system V) | Spectral class and luminosity class | Proper motion | Parallax | Radial velocity (km/sec) | Tangential velocity (km/sec) | Absolute magnitude (system V) | Luminosity (in units of solar luminosity) |
| α Canis Majoris | A1 V A5 | 1.32" | 0.375" | −8 | 17 | −1.4 +11.4 | 22.4 0.002 | |
| α Carinae | −0.75 | FO Ib–II | 0.02" | 0.018" | +20 | 5 | −4.4 | 4700 |
| α Bootis | −0.05 | K2 IIIp | 2.28" | 0.090" | −5 | 120 | −0.3 | 107 |
| α Lyrae | +0.03 | AO V | 0.34" | 0.123" | −14 | 13 | +0.5 | 51 |
| α Centauri | G2 V K5 | 3.68" | 0.751" | −22 | 23 | +4.5 +5.9 | 1.3 0.34 | |
| α Aurigae | 0.08 | G8 III | 0.44" | 0.073" | +30 | 29 | −0.6 | 141 |
| β Orionis | 0.13 | B8 Ia | 0.00" | 0.003" | +24 | 0 | −7.5 | 81,000 |
| α Canis Minoris | F5 IV-V white dwarf | 1.25" | 0.288" | −3 | 20 | +2.6 +13.1 | 7.4 0.0004 | |
| α Orionis | 0.42 var | M2 lab | 0.03" | 0.005" | +21 | 28 | −6.1 | 22,400 |
| α Eridani | 047 | B5 IV | 0.10" | 0.032" | +19 | 15 | −2.0 | 510 |
| β Centauri | 0.59 | B1 II | 0.04" | 0.016" | −12 | 11 | −3.4 | 1,860 |
| α Aquilae | 0.76 | A7 IV-V | 0.66" | 0.198" | −26 | 16 | +2.3 | 9.8 |
| α Crucis | B1 IV B1 | 0.04" | 0.008" | −6 | 24 | −4.7 4.2 | 6,200 3700 | |
| α Tauri | K5 III M2 V | 0.20" | 0.048" | +54 | 20 | −0.7 +11.8 | 155 0.0015 | |
| α Scorpii | M1 la B4 | 0.03" | 0.019" | −3 | 7 | −2.7 3.2 | 980 4.1 | |
| α Virginis | 0.97 var. | B1 V | 0.05" | 0.021" | +1 | 11 | −2.4 | 740 |
| β Geminorum | 1.14 | KO III | 0.62" | 0.093" | +3 | 32 | +1.0 | 32 |
| α Piscis Austrini | 1.16 | A3 V | 0.37" | 0.144" | +6 | 12 | +2.0 | 13 |
| α Cygni | 1.25 var. | A2 la | 0.00" | 0.003" | −3 | 0 | −6.2 | 24,600 |
| α Leonis | B7 V K2 | 0.24" | 0.039" | +3 | 29 | −0.7 +5.6 −11 | 155 0.45 0.003 | |
| Table 2. The nearest stars | ||||||
|---|---|---|---|---|---|---|
| Name | Apparent magnitude | Spectral class and luminosity class | Proper motion | Parallax | Distance (parsecs) | Absolute magnitude (system V) |
| Proxima Centauri .............. | 10.68 | M5e | 3.85" | 0.762″ | 1.31 | + 15.1 |
| α Centauri A .............. | 0.32 | G2V | 3.79″ | 0.751″ | 1.33 | + 4.76 |
| α Centauri B .............. | 1.72 | K5 V | + 6.16 | |||
| Barnard’s Star .............. | 9.54 | M5 V | 10.30″ | 0.545″ | 1.83 | + 13.22 |
| Wolf 359 .............. | 13.66 | dM6e | 4.84″ | 0.427″ | 2.34 | + 16.62 |
| BD+36°2147 .............. | 7.47 | M2V | 4.78″ | 0.396″ | 2.52 | + 10.46 |
| Sirius A .............. | -1.47 | A1 V | 1.32″ | 0.375″ | 2.66 | + 1.42 |
| Sirius B .............. | 8.67 | A5 | + 11.55 | |||
| .............. Luyten 726’8 (UV Ceti) | dM6e dM6e | 3.36″ | 0.371″ | 2.69 | + 15.3 +15.8 | |
| Ross 154 .............. | 10.6 | dM4e | 0.67″ | 0.340″ | 2.93 | + 13.3 |
| Ross 248 .............. | 12.24 | dM6e | 1.58″ | 0.316″ | 3.16 | + 14.74 |
| ∊ Eridani .............. | 3.73 | K2 V | 0.97″ | 0.303″ | 3.30 | + 6.14 |
| Ross 128 .............. | 11.13 | dM5 | 1.40″ | 0.298″ | 3.34 | + 13.50 |
| Luyten 789–6 .............. | 12.58 | dM6e | 3.27″ | 0.298″ | 3.34 | + 14.9 |
| BD Cygni A .............. | 5.19 | K5 V | 5.22″ | 0.292″ | 3.42 | + 7.52 |
| BD Cygni B .............. | 6.02 | K7 V | + 8.35 | |||
| Procyon A .............. | 0.34 | F5 IV-V | 1.25″ | 0.288″ | 3.48 | + 2.67 |
| Procyon B .............. | 10.7 | dF | + 13.1 | |||
| ∊ lndi .............. | 4.73 | K5 V | 4.67″ | 0.285″ | 3.50 | + 7.0 |
| BD+59°1915 A .............. | 8.90 | dM4 | 2.29″ | 0.278″ | 3.58 | + 11.12 |
| BD+59°1915 B .............. | 9.69 | dM5 | + 11.91 | |||
| BD+ 43°44 A .............. | 8.07 | M1 V | 2.91″ | 0.278″ | 3.58 | + 10.29 |
| BD+43°44 B .............. | 11.04 | M6 V | + 13.26 | |||
| τ Ceti .............. | 3.50 | G8 Vp | 1.92″ | 0.275″ | 3.62 | + 5.70 |
| CD-f36°15693 .............. | 7.39 | M2V | 6.87″ | 0.273″ | 3.65 | +9.57 |
| BD+5°1668 .............. | 9.82 | dM4 | 3.73″ | 0.266″ | 3.75 | + 11.95 |
| CD-39°4192 .............. | 6.72 | MO I | 3.46″ | 0.255″ | 3.90 | + 8.75 |
| Kapteyn’s Star .............. | 8.8 | sdMO | 8.79″ | 0.251″ | 3.99 | + 10.8 |
the details of the spectra). The dependence of the spectral class or color index on the effective temperature is called the effective temperature scale. If the temperature is known, then theoretically it is possible to ascertain which portion of a star’s radiation is in the invisible regions of the spectrum— ultraviolet and infrared. The absolute stellar magnitude and the correction allowing for radiation in the ultraviolet and infrared regions of the spectrum (the bolometric correction) allow the determination of the total luminosity of a star.
Stellar radii. If the effective temperature Tef and the luminosity L are known, the radius R of a star can be computed from the formula
![]()
based on the Stefan-Boltzmann law of radiation (σ is Stefan’s constant). The radii of stars with large angular dimensions may be measured directly with the aid of stellar interferometers. In eclipsing binaries it is possible to compute the values of the maximum diameters of the components expressed as fractions of the semimajor axis of their relative orbit.
Stellar rotation. The rotation of stars is studied by means of their spectra. During rotation, one edge of the star’s disk is receding from us and the other is approaching us at the same velocity. As a result, the lines are broadened in the star’s spectrum, which is simultaneously received from the whole disk, and, according to Dopplefs principle, acquire a characteristic shape from which it is possible to determine the speed of rotation. Stars of the early spectral classes O, B, and A rotate with velocities (on the equator) of at least 100–200 km/sec. The rotational velocities of cooler stars are significantly less (several km/sec). The decrease in the rotational velocity of a star is evidently connected with the transition of part of its angular momentum into the gas and dust disk surrounding it under the action of magnetic forces. Because of rapid rotation, the star assumes the form of an oblate spheroid. Radiation from stellar interiors escapes to the poles sooner than to the equator, as a result of which the temperature at the poles is higher. Therefore, a meridional flow from the poles to the equator arises on the star’s surface, and this flow circuit is completed in the deep layers of the star. This movement plays an e.ssential role in the mixing of material in layers where there is no convection.
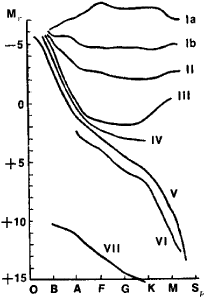
Relations between stellar parameters. Stellar masses range from 0.04 to 100 solar masses, luminosities from 5 x 10−4 to 105 solar luminosities, and radii from 2 x 10−1 to 103 solar radii. These parameters have specific interrelations. The most important of these are visualized in spectrum-luminosity (Hertzsprung-Russell) or effective temperature-luminosity diagrams. Almost all stars are situated on such diagrams along several branches, schematically depicted in Figure 2 and corresponding to different sequences or luminosity classes. The majority of stars are located on the main sequence (luminosity class V). Class O stars with temperatures of 30,000°-50,000°K form its left end, and class M red dwarfs with temperatures of 3000°-4000°K form its right end. On the diagram the sequence of giants (class III) can be seen, to which stars of high luminosity belong (that is, those with large radii). Sequences of still brighter la, Ib, and II supergiants are situated higher. (The fact that a star is a dwarf, giant, or supergiant was formerly denoted by the letters d, g, and s before the spectral class.) At the bottom of the diagram are situated white dwarfs (VII) whose sizes are comparable to the size of the earth at a density on the order of 10(i g/cm3. In addition to these fundamental sequences, subgiants (IV) and subdwarfs (VI) are also plotted.
The Hertzsprung-Russell diagram has found its explanation in the theory of the internal structure of stars.
Internal structure of stars. Inasmuch as the interiors of stars cannot be observed directly, the internal structure of stars is studied by means of constructing theoretical stellar models, which are assigned values of masses, radii, and luminosities observable in real stars. The theory of the internal structure of ordinary stars is based on the model of a star as a gaseous sphere that is in mechanical and thermal equilibrium and neither expands nor contracts over a prolonged period. Mechanical equilibrium is maintained by the forces of gravity, directed toward the center of the star, and by gas pressure in the star’s interior acting outward and balancing the force of gravity. The pressure increases with depth, and both the density and temperature increase with it. Thermal equilibrium consists in the fact that the temperature of the star—in every elementary volume—practically does not change with time, that is, the energy leaving each such volume is compensated both by the energy entering it and by the energy generated there by nuclear or other sources.
The temperature of ordinary stars varies from several thousand degrees on the surface to more than 10 million degrees in the center. At these temperatures, matter consists of almost completely ionized atoms, owing to which it becomes possible to use the equations of state of an ideal gas in the calculations of stellar models. Of great significance in the investigations of the internal stellar structure are hypotheses on energy sources, chemical composition of the stars, and the mechanism of energy transport.
The basic mechanism of energy transport in a star is radiative heat transfer. In this case, the diffusion of heat from the hotter internal regions of the star outward occurs by means of quanta of ultraviolet radiation emitted by the hot gas. These quanta are absorbed in other parts of the star and reemitted; in passing into the outer, cooler layers, the frequency of the radiation decreases. The diffusion rate is determined by the mean free path of a quantum and thus depends on the transparency of the stellar material, which in turn is characterized by its absorption coefficient. The fundamental absorption mechanisms in stars are photoelectric absorption and scattering by free electrons.
Radiative heat transfer is the basic form of energy transport for most stars. However, in certain regions of a star and over almost the entire volume of a star of small mass, an important role is played by convection, that is, the transport of heat by gas masses rising and descending under the influence of temperature differences. Convection, if it is active, is a much more effective mode of heat transport than radiative heat transfer, but convection arises only where hydrogen or helium are partially ionized: in this case, the energy of their recombination sustains the motion of the gas masses. The convection zone in the sun occupies a layer extending from the surface to a depth equal to about one-tenth of its radius; below this layer, hydrogen and helium are already completely ionized. In cool stars complete ionization occurs at greater depths, so that the convection zone in them is thicker and encompasses the greater part of the volume. In contrast, the hydrogen and helium in hot stars are completely ionized beginning almost at the surface itself, and therefore these stars do not have outer convection zones. However, they have a convection core, where the movement is sustained by the heat generated by the nuclear reactions.
Giant and supergiant stars are structured differently from main-sequence stars. Their small dense core (1 percent of the radius) contains 20–30 percent of the mass, and the remaining portion is a rarefied shell that extends out to distances of tens or hundreds of solar radii. Temperatures in the core reach 100 million degrees and more. White dwarfs are essentially just the cores of giants, but without a shell and cooled to 8,000°-10,000°K. The dense gas of cores and of white dwarfs has special properties that differ from the properties of an ideal gas. Energy in it is transported not by radiation but by electron heat conduction, as in metals. The pressure of such a gas does not depend on temperature but only on density. Therefore, equilibrium is preserved even during the cooling of a star having no energy sources.
The chemical composition of matter in the interiors of stars at early stages in their evolution is similar to the chemical composition of stellar atmospheres as determined from spectroscopic observations (diffusion separation can occur only over a period exceeding the lifetime of the star). In the course of time, nuclear reactions change the chemical composition of stellar interiors, and the internal structure of the star changes.
Stellar energy sources and the evolution of stars. The primary energy source of stars is thermonuclear reactions, in which heavier nuclei are formed from light nuclei; most often this is the transformation of hydrogen into helium. In stars of less than two solar masses it occurs chiefly by means of the fusion of two protons into a deuterium nucleus (the excess charge is carried away by a resulting positron). This is followed by the transformation of the deuterium into the isotope He3 by means of proton capture and, finally, the transformation of two He3 nuclei into a He4 and two protons. In more massive stars the carbon-nitrogen cycle predominates: carbon captures four protons in succession, emitting two positrons in the process, transforms at first into nitrogen, and then decays into helium and carbon. The final result of both reactions is the synthesis of a helium nucleus out of four hydrogen nuclei with the release of energy. The nitrogen and carbon nuclei in the carbon-nitrogen reaction act as a catalyst. In order for the nuclei to approach to a distance where capture can occur, it is necessary to overcome the electrostatic repulsion; therefore, the reactions can occur only at temperatures exceeding 1070K. These temperatures exist in the very central portions of stars. In stars of small mass, where the temperatures at the center are insufficient for thermonuclear reactions, the gravitational contraction of the star serves as a source of energy.
If the process of heat transfer and emission is known, it is possible to solve the system of equations of mechanical and thermal equilibrium and calculate out the internal structure of a star of given mass. In addition, the radius and luminosity of the star, which are functions of the mass, are also computed. The theoretical relations thus obtained can be compared to mass-luminosity and mass-radius diagrams, which are compiled from observations of stars. For main-sequence stars, the results of observations agree with theory. Stars of other sequences do not satisfy the theoretical relations. The reason for the appearance of other sequences consists in the change in the chemical composition of the interiors of stars in the process of evolution. The transformation of hydrogen into helium increases the molecular weight of the gas, resulting in core contraction and temperature increase with the gas of normal composition next to the core expanding. The star becomes a giant, while on the Hertzsprung-Russell diagram it moves along one of the lines called evolutionary tracks. Sometimes the tracks have a complex shape; moving along them, stars cross several times from one end of the diagram to the other and back. After the expansion and diffusion of the shell, the star becomes a white dwarf.
In massive stars the core at the end of evolution is unstable, and its radius decreases to approximately 10 km, where-upon the star turns into a neutron star, which consists of neutrons and not of nuclei and electrons like ordinary stars. Neutron stars have an intense magnetic field and rotate rapidly. This leads to observable bursts of radio emission, and sometimes to bursts of both optical radiation and X-radiation. Such objects are called pulsars. In still greater masses, collapse occurs—the unrestricted fall of matter toward the center with a velocity close to that of light, Part of the gravitational energy of contraction ejects a shell at a rate of up to 7,000 km/sec. During this process the star transforms into a supernova, its radiation increases to several billion times the luminosity of the sun, and then it dies gradually in the course of several months.
Binary stars. Many stars are part of binary or multiple stellar systems. If the components of binary stars are situated sufficiently far from each other, they are visible separately. These are the so-called visual binaries. Sometimes one component, the fainter one, is not visible, and the binary nature is revealed by the nonlinear motion of the brighter star. Binary stars, however, are most often recognized by the periodic splitting of their spectral lines (spectroscopic binaries) or by characteristic changes in brightness (eclipsing binaries). Many binary stars form close pairs. Mutual tidal attractions exert a substantial influence on the evolution of the components of such stars. If one of the components of a binary star expands in the process of evolution, then under certain conditions an outflow of gas begins from the point of its surface facing the other component. The gas forms streamers around the second component and partially falls into it. As a result, the first component can lose a large part of its mass and turn into a subgiant or even a white dwarf. But the second component gains part of the lost mass, and its luminosity increases correspondingly. Since this mass can include gas not only from the atmosphere but also from the deep layers near the core of the first component, anomalies in chemical composition can be observed in binary stars. However, these anomalies concern only light elements, since heavy elements do not form in giants. The heavy elements appear during the outbursts of supernovas, when many neutrons are emitted that are captured by the nuclei of atoms and increase their weight.
Peculiar and magnetic stars. Anomalies of chemical composition, which vary from place to place on the surface of a star, are often observed in so-called magnetic stars. These stars, whose spectral class is close to AO, have magnetic fields of very high intensity (up to 10,000 gauss and greater) on their surfaces. The intensity of the fields changes periodically with a mean period of from four to nine days, and the sign of the intensity also often changes. The character of the spectrum usually changes with the same period, as if the chemical composition of the star were changing. Such changes can be explained by the rotation of a star having two or more magnetic poles that do not coincide with the rotational poles. The changes in chemical composition in this case occur because more of certain elements are concentrated at the magnetic poles and more of others at the magnetic equator. In various peculiar (special) stars, characterized by the most significant peculiarities in chemical composition, the anomalies can be different; a large excess of individual elements like Si, Mg, Cr, Eu, and Mn is observed and a deficiency of He. The appearance of these anomalies is evidently caused by the suppression of convection by an intense magnetic field. In the absence of mixing, a slow diffusion of the elements under the influence of gravity and radiation pressure occurs. Certain elements sink and other elements rise, as a result of which a deficiency of the former and an excess of the latter are observed on the surface. A magnetic star rotates more slowly than an ordinary star of the same class. This is the result of the magnetic field retarding the rotation of the contracting condensate of matter out of which the star subsequently was formed.
In addition to ordinary peculiar stars there are the so-called stars with metallic lines of late spectral subclasses of A. They have a weaker magnetic field, and the anomalies in chemical composition are not as great. The nature of such stars has not yet been studied.
Certain types of anomalies, for example, an abundance of Li, are connected with the breakup of heavier nuclei by cosmic rays that are formed in the same star as a result of electromagnetic phenomena similar to chromospheric flares. These anomalies are observed, for example, in still-contracting T Tauri stars with strong convection.
Anomalies of another kind, which are observable, for example, in giants of spectral class S, are caused by the linking of a deep surface convection zone with the central convection zone, which is brought about by the intensification of nuclear reactions at a specific stage in the star’s evolution. As a result, the material of the entire star is mixed, and elements synthesized in its central regions are carried outward.
Variable stars. The brightness of many stars is not constant and varies in accordance with one law or another; these stars are called variable stars. Stars in which the changes in brightness are connected with physical processes occurring in them are physical variables (as distinguished from optical variables, which include eclipsing binaries). Periodic and semiperiodic variability is usually associated with the pulsations of stars, and sometimes with large-scale convection. Generally speaking, stars, as systems in stable equilibrium, are characterized by pulsations with their distinctive periods. Oscillations can arise in the process of rearrangement in a star’s structure, which is connected with evolutionary changes. However, to prevent damping, mechanisms must exist that sustain or intensify them: during the period of maximum contraction of the star, it needs to receive the thermal energy that would escape outward during the period of expansion. In agreement with modern theories, the pulsations of many types of variables (cepheids, RR Lyrae type variables) are explained by an increase in the absorption coefficient during the star’s contraction; this inhibits the total flux of radiation, and the gas receives additional energy. During expansion, the absorption decreases and the energy escapes outward. The inhomogeneous structure of a star—the presence of several layers with different properties—distorts the normal pattern and produces deviations from a truly sinusoidal behavior of the star’s parameters. A fundamental standing wave is often located in the depths of the star, and it generates traveling waves that emerge at the surface and affect the phases of the variations in brightness, velocity, and other parameters.
Certain types of variable stars undergo outbursts during which the brightness increases by 10–15 magnitudes (so-called novas), by 7–8 magnitudes (recurrent novas), or by 3–4 magnitudes (novalike stars). Such outbursts are associated with a sudden expansion of the photosphere with great velocities (up to 1,000–2,000 km/sec in novas) that leads to ejection of the shell with a mass of about 10~5–10~4 solar masses. After the outburst the brightness begins to decrease with a characteristic time of 50–100 days. During this time the escape of gases from the surface continues with a velocity of several thousand km/sec. All these stars prove to be close binaries, and their outbursts are undoubtedly related to the interaction of the components of the system, one or both of which are usually hot dwarfs. The intense magnetic field of the stars apparently influences the structure of the shells ejected by novas. The rapid irregular variability of T Tauri, UV Ceti, and other types of young contracting stars is linked to powerful convection movements in these stars, which carry hot gas to the surface. The previously mentioned supernovas may also belong to the class of variable stars. The Milky Way Galaxy numbers more than 30,000 variable stars.
Work on the study of stars is being conducted in the USSR at the Crimean Astrophysical Observatory of the Academy of Sciences of the USSR, at the Central Astronomical Observatory of the Academy of Sciences of the USSR, at the P. K. Shternberg State Astronomical Institute, at the Astronomical Council of the Academy of Sciences of the USSR, and at other astronomical institutions. Reports on these studies are published in the journals Astronomicheskii Zhurnal and Astrofizika and in publication of the observatories. Abroad, investigations of stars are conducted in the USA, Great Britain, Australia, and many other countries. The principal journal in the foreign literature is Astrophysical Journal (USA), and there are a number of other important publications in the USA, Great Britain, and other countries.
REFERENCES
Frank-Kamenetskii, D. A. Fizicheskie protsessy vnutri zvezd. Moscow, 1959.Mustel’, E. R. Zvezdnye atmosfery. Moscow, 1960.
Schwarzschild, M. Stroenie i evoliutsiia zvezd. Moscow, 1961. (Translated from English.)
Gorbatskii, V. G., and I. N. Minin. Nestatsionarnye zvezdy. Moscow, 1963.
Zvezdnye atmosfery. Edited by J. L. Greenstein. Moscow, 1963. (Translated from English.)
Kaplan, S. A. Fizika zvezd, 2nd ed. Moscow, 1970.
Pul’siruiushchie zvezdy. Moscow, 1970.
Martynov, D. la. Kurs obshchei astrofiziki, 2nd ed. Moscow, 1971.
S. B. PIKEL’NER
Star’
an urban-type settlement in Diat’kovo Raion, Briansk Oblast, RSFSR. Located 11 km from the Diat’kovo railroad station on the Briansk-Viaz’ma line, Star’ has a glass plant.