inequality

inequality

1. Maths

a. a statement indicating that the value of one quantity or expression is not equal to another, as in x ≠ y

b. a relationship between real numbers involving inequality: x may be greater than y, denoted by x > y, or less than y, denoted by x < y

2. Astronomy a departure from uniform orbital motion

Collins Discovery Encyclopedia, 1st edition © HarperCollins Publishers 2005

inequality

An irregularity in the orbital motion of a celestial body. The inequalities of the Moon's motion are periodic terms whose sum gives the variation of either the spherical coordinates or the osculating elements of the lunar orbit. The principal inequalities of the Moon's motion are evection and variation.

Collins Dictionary of Astronomy © Market House Books Ltd, 2006

inequality

See EQUALITY.

Collins Dictionary of Sociology, 3rd ed. © HarperCollins Publishers 2000

inequality

[‚in·i′kwäl·əd·ē]

(mathematics)

A statement that one quantity is less than, less than or equal to, greater than, or greater than or equal to another quantity.

McGraw-Hill Dictionary of Scientific & Technical Terms, 6E, Copyright © 2003 by The McGraw-Hill Companies, Inc.

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Inequality

 

(mathematics), a relation between two numbers or quantities indicating which of them is greater or smaller. An inequality is denoted by the symbol <, which is drawn pointed toward the smaller number. Thus, 2 > 1 and 1 < 2 state the same thing, namely, 2 is greater than 1 and 1 is less than 2. Sometimes we make use of multiple inequalities as in a < b < c. In order to express the fact that of two numbers a and b, the first is greater than or equal to the second, we write a ≥ b (or b ≤ a) and read “a is greater than or equal to b” (or “a is less than or equal to b“ or simply “a is not less than b“ (or “b is not greater than a”). The notation α ≠ b signifies that the numbers a and b are unequal but does not indicate which is larger. All these relations are termed inequalities.

Inequalities have many properties in common with equalities. Thus, an inequality remains valid if the same number is added to or subtracted from both sides. We can similarly multiply both sides of an inequality by a positive number. However, if both sides are multiplied by a negative number, then the sense of the inequality is reversed, that is, the symbol > is replaced by <, and < by >. From the inequalities A < B and C < D follow the inequalities A + C < B + D and A —D < B —C; in other words, inequalities of the same sense (A < B and C < D) may be added term by term, and inequalities of opposite sense (A < B and D > C) may be subtracted term by term. If the numbers A, B. C, and D are positive, then the inequalities A < B and C < D also imply AC < BD and A/D < B/C; in other words, inequalities of the same sense (between positive numbers) may be multiplied term by term, and those of opposite sense may be divided term by term.

Inequalities containing quantities that can assume different numerical values may be true for some values of these quantities and false for others. Thus, the inequality x² —4x + 3 > 0 is true for x = 4 and false for x = 2. To solve such inequalities is to determine the limits within which the quantities entering into the inequalities must be taken in order for the inequalities to hold. Thus, by rewriting the inequality x² —4x + 3 > 0 in the form (x —1) (x —3) > 0, we see that the latter holds for all x satisfying either one of the inequalities x < 1, x > 3, and these yield the solution of the original inequality.

We now give a few examples of important inequalities.

(1) “Triangle” inequality. For any real or complex numbers a₁, a₂, . . . ,a_n,

ǀa₁ + a₂ + . . . a_nǀ ≤ ǀa₁ǀ + ǀa₂ǀ + . . . + ǀa_nǀ

(2) Inequality for means. The most famous inequality relates the harmonic mean, the geometric mean, the arithmetic mean, and the root-mean-square:

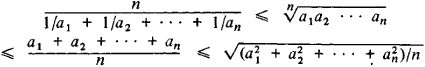
The numbers a₁, a₂, . . . , a_n are assumed to be positive.

(3) Linear inequalities. Consider the system of inequalities

a_i1x₁ + a_i2x₂ + . . . + a_in x_n ≥ b_i

(i = 1, 2, . .. ,m)

The totality of solutions of this system is a convex polyhedron in n-dimensional space (x₁,x₂, . . . x_n). The task of the theory of linear inequalities consists of studying the properties of this polyhedron. Certain problems in the theory of linear inequalities are closely related to the theory of best approximations, which was created by P. L. Chebyshev.

(See also, , , , and .)

Inequalities are very important in many branches of mathematics. Diophantine approximations, an entire branch of number theory, are completely based on inequalities. Analytic number theory often operates with inequalities. The axiomatic development of inequalities is given in algebra. Linear inequalities play a large role in the theory of linear programming. In geometry, inequalities are constantly encountered in the theory of convex bodies and in isoperimetric problems. In probability theory, many laws are formulated in terms of inequalities (for example, the Chebyshev inequality). Differential inequalities are used in the theory of differential equations (the Chaplygin method). In the theory of functions, various inequalities are constantly used for derivatives of polynomials and trigonometric polynomials. In functional analysis, the definition of norm in a function space requires that it satisfy the triangle inequality

ǀǀx + y ǀǀ ≤ ǀǀxǀǀ + ǀǀyǀǀ

Many classical inequalities virtually define or estimate the norm of a linear functional or a linear operator in some space.

REFERENCES

Korovkin, P. P. Neravenstva, 3rd ed. Moscow, 1966. Hardy, G. H. , S. E. Littlewood, and G. Pólya. Neravenstva. Moscow, 1948. (Translated from English.)

The Great Soviet Encyclopedia, 3rd Edition (1970-1979). © 2010 The Gale Group, Inc. All rights reserved.