orientation
Orientation


family of origin
ororientation
the NUCLEAR, or EXTENDED FAMILY within which a person was raised. As a chief agent of SOCIALIZATION, the family of origin provides the social, cultural and linguistic background with which the person may continue to identify and be influenced by throughout life.orientation
[‚ȯr·ē·ən′tā·shən]orientation
orientation
ii. Turning the instrument or map until the datum point or meridian is aligned with the datum point or true meridian on earth.
orientation
In typography, the direction of print across a page. See portrait and orientation agnostic.Orientation
a generalization of the concept of direction on a line to more complex geometrical figures.
Orientation on a line. A point can move along a line in two opposite directions. For example, on the horizontal line AB (Figure 1,a) it is possible to move either from right to left or from left to right. A line that has a specific direction indicated on it is termed an oriented line.
Orientation on a curve. Analogously to orientation on a line, every closed curve can be oriented either counterclockwise (Figure 1,b) or clockwise (Figure 1,c).
Orientation in a plane. If a region of a plane is bounded by a simple closed curve, that is, a closed curve free of multiple points, the curve can be oriented in two different directions. Orienting the curve orients the plane region the curve bounds. Two simple closed curves in a plane are considered to be identically oriented if when the curves are traversed in the indicated direction, the plane regions the curves bound remain on the same side, in both cases either on the right or on the left. For example, the curves in Figure 1,b and 1,d are oriented in the same direction, but the curve in Figure 1,c has an opposite orientation. It is sufficient to choose the orientation of a single closed curve on the plane in order to define the corresponding orientation of all other such curves lying in the same plane.
A plane for which a specific orientation has been chosen for the simple closed curves it contains is called an oriented plane. Each plane can be oriented in two directions. The orientation of a plane can also be given by choosing a system of Cartesian coordinates. If the x-axis and the y-axis are chosen with specific positive directions, this choice corresponds to an orientation of the plane such that a circle centered on the origin is oriented in the direction from the positive x-axis to the positive y-axis. For example, the coordinate systems in Figure 1,e and 1,f define the

same orientation of the plane. The coordinate system in Figure 1,g is oriented in the opposite direction.
The coordinates (x, y) and (x′, y′) in two rectangular coordinate systems on the plane are linked by the relations
x′ = a11x + a12 + b1
y′ = a21x + a22 + b2
where the determinant
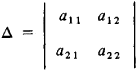
is nonzero. The coordinate systems (x, y) and (x′, y′) are oriented in the same direction if Δ > 0 and in opposite directions if Δ < 0. This fact can be used to construct a rigorous analytic theory of orientation on the plane. It is easy to see that the set S of all rectangular coordinate systems can be divided into two subsets S′ and S″ such that all the coordinate systems in S′ are related by transformations with Δ > 0, as are all the systems in S″, and any coordinate system in S′ is related to a coordinate system in S′ by a transformation with Δ < 0. Choosing an orientation of the plane means choosing one of the sets S″ or S″. The choice of orientation on a plane determines the signs of angles located in the plane and of the areas bounded by oriented closed curves. For example, the formula
![]()
for the area s bounded by the closed curve c, which is oriented in the direction indicated by the arrow, leads in a right-handed coordinate system (Figure 1,e and 1,0 to a positive area for Figure 1,b and 1,d and to a negative area for Figure 1,c. Conversely, in a left-handed coordinate system (Figure 1,g) the area s, as computed by the above formula, will be positive for Figure 1,c and negative for Figure 1,b and 1,d.
Orientation of a surface. The orientation of any surface dividing space into two parts, for example, a sphere, can be defined in a manner similar to the above definition of the orientation of a plane. Let us consider regions of the surface that are bounded by simple closed curves. To orient such a surface region means to choose a specific orientation for the curve bounding the region. Two regions of a surface are said to be oriented the same way if when the curves bounding the regions are traversed in the indicated direction the regions remain on the same side. For example, the surfaces of the two cubes in Figure 1,h and 1,i are oriented in the same direction, but the surface of the cube in Figure 1,j is oriented in the opposite direction. A surface on which regions bounded by simple closed curves have a specific orientation is called an oriented surface. Not all surfaces can be oriented. Surfaces that bound a region of space, however, are always orientable.
Orientation of a space. When a closed surface bounds a certain region of three-dimensional space, the surface is said to have a right-handed orientation if its regions are oriented counterclockwise when viewed from the outside, like the cubes in Figure 1,h and 1,i. Conversely, the orientation of a closed surface bounding a region of space is considered to be left-handed if regions of the surface are oriented in a clockwise direction when viewed from outside, like the cube in Figure 1,j. The choice of a specific orientation for closed surfaces that lack self-intersections yields the orientation of the space. Thus, there are two possible orientations for three-dimensional space: right-handed and left-handed.
The orientation of three-dimensional space may also be established by choosing a system of Cartesian coordinates. Suppose we choose an x-axis, a y-axis, and a z-axis on each of which a positive direction is defined. The corresponding orientation of the space is then defined in the following way. Consider any tetrahedron OABC with vertex O at the origin and vertices A, B, and C lying, respectively, on the positive x-, y-, and z-axes (Figure 1,k and 1,1), and assume that the triangle ABC on the surface of the tetrahedron is oriented in the order ABC, that is, from the x-axis to the y-axis and then to the z-axis. The orientation of the tetrahedron’s surface is thereby defined, as is, consequently, the orientation of the entire space. The choice of axes in Figure 1,k corresponds to a right-handed orientation of space, and the choice in Figure 1,1 corresponds to a left-handed orientation of space. This principle divides the coordinate systems in space into right-handed and left-handed systems. The choice of spatial orientation determines the sign of volumes bounded by oriented surfaces, the sense of the vector product of two vectors, and so forth.
Both left-handed and right-handed coordinate systems are used in scientific literature. For example, a left-handed system is widely used in Soviet works on mathematics, while a right-handed system is used in engineering and physics.
The concept of orientation can be extended to multidimensional spaces.
Orientation
the determination of one’s position relative to the points of the compass by means of a compass, map, or aerial photograph. Approximate orientation is possible using local natural and artificial points of reference or the position of the sun, moon, and stars, as well as with the aid of radio, light, and sound signals.