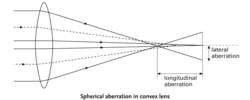
spherical aberration

Spherical aberration in convex lens

spherical aberration

(sfe -ră-kăl) (SA) An aberration of a spherical lens or mirror in which light rays converge not to a single point but to a series of points whose distances from the lens or mirror decrease as the light rays fall nearer the periphery of the optical element (see illustration). It is most obvious with elements of large diameter. It can be considerably reduced by using an aplanatic system, which also reduces coma, or by using a correcting plate. Paraboloid surfaces are free of spherical aberration, but not of coma. See also Schmidt telescope.

Collins Dictionary of Astronomy © Market House Books Ltd, 2006

spherical aberration

[′sfir·ə·kəl ‚ab·ə′rā·shən]

(optics)

Aberration arising from the fact that rays which are initially at different distances from the optical axis come to a focus at different distances along the axis when they are reflected from a spherical mirror or refracted by a lens with spherical surfaces.

McGraw-Hill Dictionary of Scientific & Technical Terms, 6E, Copyright © 2003 by The McGraw-Hill Companies, Inc.

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Spherical Aberration

 

a type of aberration of optical systems. In spherical aberration, rays of light that pass through an axisymmetric optical system, such as a lens, at different distances from the system’s optical axis are not brought to a common focus (Figure 1). Paraxial rays passing through the central zone h₀h₁ of the system come to a focus in the Gaussian image plane Oh. Rays passing through other zones, such as h₁h₂ and h₂h₃, are focused closer than the Gaussian plane in the case of converging, or positive, systems and farther away than the Gaussian plane in the case of diverging, or negative, systems.

As a result of spherical aberration, the image produced by parallel object rays on a screen perpendicular to the axis at the point O has the form not of a point but of a disk, called the circle of confusion, with a bright core and a fainter halo. When the screen is moved along the optical axis, the size of the circle of confusion

Figura 1. Spherical aberration of a converging, or positive, lens

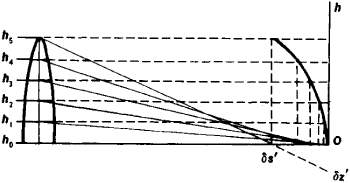
and the distribution of illuminance in the circle are changed. At a certain position of the screen, the size of the circle of confusion is at a minimum, and we speak of the circle of least confusion. The diameter of the circle of least confusion is approximately one-fourth of that of the circle in the Gaussian plane.

A distinction is made between longitudinal and lateral spherical aberration. The longitudinal spherical aberration is equal to the length of the segment Oδs’ measured from the Gaussian plane to the point where the rim rays—that is, the rays passing through the outer zone at the rim of the optical system (h₄h₅ in Figure 1)—come to a focus. The lateral spherical aberration is equal to the radius of the circle of confusion Oδz’ in the Gaussian plane; this radius is determined by the rays coming from the outer zone h₄h₅.

Since for converging lenses Oδs’ < 0 and for diverging lenses Oδs’ > 0, spherical aberration can be almost completely eliminated by using a certain combination of lenses in the optical system. In the case of an individual lens with spherical surfaces, the spherical aberration can be reduced by using surfaces that exhibit an optimum ratio of their radii of curvature. If the refractive index of the material of the lens is 1.5, the spherical aberration is at a minimum when this ratio is 1/6. Spherical aberration can also be reduced by using optical elements with aspherical, for example, parabolic, surfaces.

REFERENCES

Tudorovskii, A. N. Teoriia opticheskikh priborov, part 1. Moscow-Leningrad, 1948.
Rusinov, M. M. Tekhnicheskaia optika. Moscow-Leningrad, 1961.
Volosov, D. S. Fotograficheskaia optika. Moscow, 1971.

L. N. KAPORSKII

The Great Soviet Encyclopedia, 3rd Edition (1970-1979). © 2010 The Gale Group, Inc. All rights reserved.