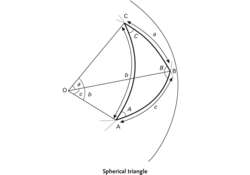
spherical triangle

A triangle on the surface of a sphere formed by the intersections of three great circles (see illustration). The arcs BC, AC, and AB form the sides of the spherical triangle ABC. The lengths of these sides (a , b , and c ), in angular measure, are equal to the angles BOC, COA, and AOB, respectively, where O is the center of the sphere. This assumes a radius of unity. The angles between the planes are the spherical angles A, B, and C of the triangle.

The relationships between the angles and sides of spherical triangles are extensively used in astrometry. The three basic relationships are the sine formula:

sin A /sin a = sin B /sin b = sin C /sin c

the cosine formula:

cos a = cos b cos c + sin b sin c cos A

cos b = cos a cos c + sin a sin c cos B

cos c = cos a cos b + sin a sin b cos C

and the extended cosine formula, which can be derived from the other two.

For a spherical right-angled triangle, in which one angle, say C, is equal to 90° so that sin C = 1, cos C = 0, the formulae are much simplified. They are also simplified if the sides of the triangle are small so that, say, sin a tends to a and cos a to 1–a ²/2. As a , b , and c approach zero the formulae reduce to those used in plane geometry. The formulae may be extended by replacing the sides and angles by the supplements of the corresponding angles and sides, respectively. Thus

sin A = sin a, cos A = –cos a

Collins Dictionary of Astronomy © Market House Books Ltd, 2006

spherical triangle

[′sfir·ə·kəl ′trī‚aŋ·gəl]

(mathematics)

A three-sided surface on a sphere the sides of which are arcs of great circles.

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Spherical Triangle

a geometric figure formed by arcs of three great circles connecting any three points on a sphere in pairs.

Mentioned in

References in periodicals archive

Every visible triangle is indistinguishable from some spherical triangle, and therefore (by P1) has its visible angles equal to the visible angles in the spherical triangle.

The visible angles in a spherical triangle equal its real angles (from P2).

The real angles in a spherical triangle add up to more than 180 degrees.

To the eye looking out from the center of the sphere, the resulting plane triangle will be indistinguishable from the original spherical triangle (in the sense that one perfectly occludes the other), but it will be a 60-60-60 triangle rather than a 90-90-90 triangle.

The argument is a theoretical argument showing that the angles in any visible triangle are not "strictly and mathematically" equal to the angles in any Euclidean plane triangle, but are equal to the angles in a spherical triangle instead.

Reid would still be able to maintain that the visible triangle presented to us by three such lines of varying brightness or dimness has the angle sum of a spherical triangle.

Visible triangles are indistinguishable from spherical triangles. In particular, for every visible triangle v seen from e, there is a spherical triangle s centered on e such that the apparent magnitudes of angles in v are equal to the apparent magnitudes of angles in s.

In a spherical triangle, the apparent magnitudes of the angles (as seen from the center of the sphere) are equal to their real magnitudes.

The real magnitudes of the angles of a spherical triangle sum to more than 180 degrees.

It is rather that visible triangles have angles that appear equal to the angles in a spherical triangle with certain numerical magnitudes.

Thomas Reid's geometry of visibles

This month, we will run through the basic relationships in spherical triangles. Next month, we will apply spherical trigonometry to several practical EW problems.

Right spherical triangles allow the use of a set of simplified trigonometric equations generated by Napier's rules.

Tutorial on Spherical Trigonometry for EW Applications