velocity

velocity

Physics a measure of the rate of motion of a body expressed as the rate of change of its position in a particular direction with time. It is measured in metres per second, miles per hour, etc.

Collins Discovery Encyclopedia, 1st edition © HarperCollins Publishers 2005

Velocity

The time rate of change of position of a body in a particular direction. Linear velocity is velocity along a straight line, and its magnitude is commonly measured in such units as meters per second (m/s), feet per second (ft/s), and miles per hour (mi/h). Since both a magnitude and a direction are implied in a measurement of velocity, velocity is a directed or vector quantity, and to specify a velocity completely, the direction must always be given. The magnitude only is called the speed. See Speed

A body need not move in a straight line path to possess linear velocity. When a body is constrained to move along a curved path, it possesses at any point an instantaneous linear velocity in the direction of the tangent to the curve at that point. The average value of the linear velocity is defined as the ratio of the displacement to the elapsed time interval during which the displacement took place.

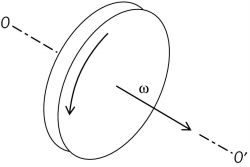
The representation of angular velocity ω as a vector is shown in the illustration. The vector is taken along the axis of spin. Its length is proportional to the angular speed and its direction is that in which a right-hand screw would move. If a body rotates simultaneously about two or more rectangular axes, the resultant angular velocity is the vector sum of the individual angular velocities.

Angular velocity shown as an axial vector

McGraw-Hill Concise Encyclopedia of Physics. © 2002 by The McGraw-Hill Companies, Inc.

velocity

[və′läs·əd·ē]

(mechanics)

The time rate of change of position of a body; it is a vector quantity having direction as well as magnitude. Also known as linear velocity.

The speed at which the detonating wave passes through a column of explosives, expressed in meters or feet per second.

McGraw-Hill Dictionary of Scientific & Technical Terms, 6E, Copyright © 2003 by The McGraw-Hill Companies, Inc.

velocity

The rate of change of position in a given direction.

An Illustrated Dictionary of Aviation Copyright © 2005 by The McGraw-Hill Companies, Inc. All rights reserved

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Velocity

 

in mechanics, a kinematic quantity characterizing the motion of a point. Strictly speaking, velocity is a vector quantity and thus has both a magnitude and a direction. The magnitude, a scalar quantity, is known as speed. The term “velocity,” however, is sometimes loosely used in the sense of “speed.”

For a point in uniform motion, its speed v is equal to the ratio of the distance s traversed to the time t in which this distance is traveled—that is, v = s/t. In the general case, the instantaneous speed of a point is v = ds/dt, and the instantaneous velocity is v = dr/dt, where r is the radius vector of the point. The velocity vector is directed along the tangent to the point’s trajectory. If the motion of the point is defined by equations that express the dependence of the point’s Cartesian coordinates x, y, and z on the time t, then

where v_x = dx/dt, v_y= dy/dt, and v_z = dz/dt. The cosines of the angles formed by the velocity vector and the coordinate axes are equal to v_x/v_x v_y/v_z and v_z/v, respectively.

The Great Soviet Encyclopedia, 3rd Edition (1970-1979). © 2010 The Gale Group, Inc. All rights reserved.