hyperbolic functions

[¦hī·pər¦bäl·ik ′fəŋk·shənz]

(mathematics)

The real or complex functions sinh (x), cosh (x), tanh (x), coth (x), sech (x), csch (x); they are related to the hyperbola in somewhat the same fashion as the trigonometric functions are related to the circle, and have properties analogous to those of the trigonometric functions.

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Hyperbolic Functions

functions defined by the equations

sinh x = (hyperbolic sine of x)

cosh x = (hyperbolic cosine of x)

In some cases, the hyperbolic tangent is also considered:

tanh x =

(See Figure 1 for graphs of the hyperbolic functions.) Hyperbolic functions are connected by relations similar to those connecting the trigonometric functions:

cosh²x - sinh² = 1

tanh x = sinh x/cosh x

sinh (x±y) = sinh x cosh y ± cosh x sinh y

cosh (x±y) = cosh x cosh y ± sinh x sinh y

Figure 1

Figure 2

Hyperbolic functions may be expressed in terms of trigonometric functions:

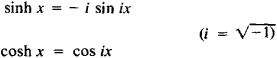
Geometrically, the hyperbolic functions are obtained by analysis of the rectangular hyperbola x² - y² = 1, which may be defined in terms of the parametric equations x = cosh t and y = sinh t. The argument t represents twice the area of the hyperbolic sector OAC (see Figure 2). Inverse hyperbolic functions are defined by the equations

REFERENCE

Ianpol’skii, A. R. Giperbolicheskie funktsii. Moscow, 1960.