sequence

sequence

1. 

a. Cards a set of three or more consecutive cards, usually of the same suit

b. Bridge a set of two or more consecutive cards

2. Music an arrangement of notes or chords repeated several times at different pitches

3. Maths

a. an ordered set of numbers or other mathematical entities in one-to-one correspondence with the integers 1 to n

b. an ordered infinite set of mathematical entities in one-to-one correspondence with the natural numbers

4. a section of a film constituting a single continuous uninterrupted episode

5. Biochem the unique order of amino acids in the polypeptide chain of a protein or of nucleotides in the polynucleotide chain of DNA or RNA

6. RC Church another word for prose

Collins Discovery Encyclopedia, 1st edition © HarperCollins Publishers 2005

sequence

[′sē·kwəns]

(computer science)

To put a set of symbols into an arbitrarily defined order; that is, to select A if A is greater than or equal to B, or to select B if A is less than B.

(engineering)

An orderly progression of items of information or of operations in accordance with some rule.

(geology)

A sequence of geologic events, processes, or rocks, arranged in chronological order.

A geographically discrete, major informal rock-stratigraphic unit of greater than group or supergroup rank. Also known as stratigraphic sequence.

A body of rock deposited during a complete cycle of sea-level change.

(mathematics)

A listing of mathematical entities x₁, x₂… which is indexed by the positive integers; more precisely, a function whose domain is an infinite subset of the positive integers. Also known as infinite sequence.

(meteorology)

collective

McGraw-Hill Dictionary of Scientific & Technical Terms, 6E, Copyright © 2003 by The McGraw-Hill Companies, Inc.

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Sequence

 

a fundamental concept of mathematics. A sequence is a set of elements of any nature that are ordered as are the natural numbers 1,2,…, n…. It can be written in the form x₁, x₂, …, x_n, … or simply {x_n}. The elements of which it is composed are called its terms. Different terms of a sequence may be identical.

A sequence may be regarded as a function whose argument can take on only positive integral values—that is, a function defined on the set of natural numbers. To define a sequence, we can either specify its nth term or make use of a recurrence formula, by which each term is defined as a function of preceding terms. Fibonacci numbers, for example, are defined through a recurrence formula. The sequences most often encountered are those of numbers or functions. For example,

(1) 1, 2, …, n, …

that is, x_n = n

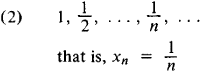
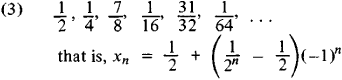
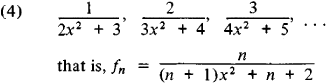
If the terms of a sequence of numbers differ by an arbitrarily small amount from the number a for sufficiently large n, the sequence is said to be convergent, and a is called its limit. The limit of a sequence of functions is defined in a similar manner. For example, sequences (2) and (4) are convergent, and their limits are 0 and the function 1/(1 + x²), respectively. Sequences that are not convergent are said to be divergent. Sequences (1) and (3) are examples of divergent sequences.

The Great Soviet Encyclopedia, 3rd Edition (1970-1979). © 2010 The Gale Group, Inc. All rights reserved.