Moment of Force

moment of force

[′mō·mənt əv ′fȯrs]

(mechanics)

torque

McGraw-Hill Dictionary of Scientific & Technical Terms, 6E, Copyright © 2003 by The McGraw-Hill Companies, Inc.

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Moment of Force

 

a quantity that characterizes the rotational effect of a force acting on a rigid body; the moment of a force is a fundamental concept of mechanics. A distinction is made between the moment of a force about a center (a point) and about an axis.

The moment of a force about a center O is a vector quantity. The magnitude of the moment is MO = Fh, where F is the force and h is the arm, that is, the length of the perpendicular drawn from O to the line of action of the force (see Figure 1); the vector MO is perpendicular to the plane that contains the center O and the force F and is pointed in a direction such that the rotation caused by the force appears counterclockwise (in a right-handed coordinate system). The moment of a force is expressed as a vector product, by the equation M_O = [rF], where r is the radius vector drawn from O to the point of application

Figure 1

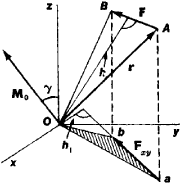
of the force. The dimensions of the moment of a force are L²MT², and the units of measurement are newton ⋅ meters (n ⋅ m), dyne ⋅ cm (1 N ⋅ m = 10⁷ dyne ⋅ cm), or kilogram-force ⋅ meters.

The moment of a force about an axis is a scalar quantity equal to the projection, on this axis, of the moment of the force about any point O of the axis or equal to the numerical value of the moment of the projection F_xy of the force F on the xy-plane, which is perpendicular to the z-axis, taken with respect to the point of intersection of the axis with the plane. In other words,

MZ = M₀ cos γ = ± F_xyh₁

The plus sign in this expression is selected when the rotation caused by the force F is counterclockwise when viewed from the positive end of the z-axis (also in a right-handed system). The moments of a force about the x-, y-, and z-axes can also be calculated from the formulas

M_x = YF_z − ZF_yM_y = zF_x − xF_z

where F_x, F_y, and F_z are the projections of the force F on the axes; x,y, and z are the coordinates of the point A of application of the force.

If a system of forces has a resultant, then the moment of the system is calculated according to Varignon’s theorem.

S. M. TARG

The Great Soviet Encyclopedia, 3rd Edition (1970-1979). © 2010 The Gale Group, Inc. All rights reserved.