momentum

1. Physics the product of a body's mass and its velocity.

2. the impetus of a body resulting from its motion

Collins Discovery Encyclopedia, 1st edition © HarperCollins Publishers 2005

Momentum

Linear momentum is the product of the mass and the linear velocity of a body. It is defined by Eq. (1),

(1)

where m is the mass and v is the linear velocity. Since linear momentum is the product of a scalar and a vector quantity, it is a vector and hence has both magnitude and direction.

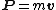
According to the general statement of Newton's second law, for a force F , a momentum P , and a time t, Eq. (2) holds.

(2)

Thus Newton's second law involves the time rate of change of momentum. Changes of momentum are important in collision processes. See Collision (physics)

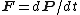
When a group of bodies is subject only to forces that members of the group exert on one another, the total momentum of the group remains constant. See Angular momentum, Conservation of momentum, Impulse (mechanics)

momentum

1. (linear momentum) Symbol: p. A property of a body moving in a straight line. It is equal in magnitude to the product of the mass and velocity of the body. It is a vector quantity, mv , having the same direction as the velocity. See also conservation of momentum; Newton's laws of motion.

2. See angular momentum.

Collins Dictionary of Astronomy © Market House Books Ltd, 2006

momentum

[mō′ment·əm]

(mechanics)

Also known as linear momentum; vector momentum.

For a single nonrelativistic particle, the product of the mass and the velocity of a particle.

For a single relativistic particle, m v/(1 -v ²/ c ²)^1/2, where m is the rest-mass,vthe velocity, and c the speed of light.

For a system of particles, the vector sum of the momenta (as in the first or second definition) of the particles.

momentum

Of a moving body, the product of the mass of the body and its velocity.

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Momentum

a measure of mechanical motion that for a mass point is equal to the product of the mass m of the point and its velocity v. Momentum, mv, is a vector quantity, with the same direction as the velocity of the point. Upon the action of a force, the momentum of the point changes, usually both numerically and in direction. This change is determined by the second (basic) law of dynamics.

The momentum Q of a mechanical system is equal to the geometric sum of the momentums of all its points or the product of the mass M of the entire system and the velocity v_c of its center of mass: Q = Σ m_kv_k = Mv_c. A change in the momentum of the system takes place only through the action of external forces—that is, forces acting on the system from bodies that are not part of the system. According to the theory of the change of momentum, Q₁ – Q₀ = ΣS_k^e, where Q₀ and Q₁ are the momentums of the system at the beginning and end of a certain time interval and S_k^e are the momentums of external forces F_k^e over the time interval (this theorem is expressed in differential form by the equation dQ/dt = ΣF_k^e). This theorem is used for the solution of many problems in dynamics, particularly in impact theory.

For a closed system (that is, for a system that does not experience external forces), or in the case in which the geometric sum of the external forces acting on the system equals zero, the law of conservation of momentum is valid. In such cases the momentums of the individual parts of the system (for example, during the action of internal forces) may change, but in such a way that the quantity Q = Σ m_kv_k remains constant. This law explains such phenomena as jet propulsion, the recoil upon firing a gun, and the operation of a screw propeller or oars. For example, if a gun and bullet are regarded as a single system, then the pressure of the powder gases upon firing will be an internal force for the system and cannot change the momentum of the system, which was equal to zero before the firing. Therefore, in imparting the momentum m₁v₁ to the bullet in the direction toward the muzzle, the powder gases simultaneously impart to the gun a momentum m₂v₂, which is numerically equal but opposite in direction, resulting in the recoil. If the velocity v₁ of the bullet upon its exit from the barrel is known, the maximum recoil velocity v₂ may be found from the equation m₁v₁ = m₂v₂ (Where v₁ and v₂ are scalar quantities of velocity).

At velocities close to the speed of light c, the momentum of a free particle is given by the formula , where β = v/c. When ν << c, this formula becomes the ordinary formula p = mv.

Momentum exists for physical fields (electromagnetic, gravitational, and so on). The momentum of a field is characterized by momentum density (the relationship of the momentum of a unit volume to the entire volume) and is expressed as field intensity or field potential.

S. M. TARG