parallax

1. an apparent change in the position of an object resulting from a change in position of the observer

2. Astronomy the angle subtended at a celestial body, esp a star, by the radius of the earth's orbit. Annual or heliocentric parallax is the apparent displacement of a nearby star resulting from its observation from the earth. Diurnal or geocentric parallax results from the observation of a planet, the sun, or the moon from the surface of the earth

Collins Discovery Encyclopedia, 1st edition © HarperCollins Publishers 2005

parallax

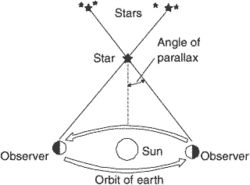
(pa -ră-laks) The angular displacement in the apparent position of a celestial body when observed from two widely separated points. It is thus the angle that the baseline connecting two viewpoints would subtend at the object (see illustration). It is very small in value and is usually expressed in arc seconds. If the baseline is of a fixed length then as the distance to the celestial object decreases, its parallax will increase accordingly. If the parallax can be measured then so can the distance.

The observer's position on Earth changes with the daily rotation of the Earth, the annual revolution of the Earth around the Sun, and the long-term motion of the Sun and Solar System relative to the background stars. Each motion produces a different measure of parallax: diurnal parallax, annual parallax, and secular parallax, respectively. The continual change in the apparent position of a celestial object, produced by the observer's changing position, is termed parallactic motion and must be distinguished from the star's own peculiar motion in space.

Methods used to determine the parallax and hence the distance of celestial bodies require an accurate knowledge of the baseline length. The baseline for diurnal parallax – the Earth's radius – can be used for distance measurements only within the Solar System. The baselines used in annual parallax – the semimajor axis of the Earth's orbit – and secular parallax are sufficiently great for stellar distances to be measured. Other methods based on the concept of parallax and used in distance determination include dynamical parallax, moving-cluster parallax, and statistical parallax.

Distances determined indirectly from stellar brightness are also sometimes called parallaxes: in spectroscopic parallax the absolute magnitude of a main-sequence star is deduced from the spectral type of the star using the Hertzsprung–Russell diagram and this together with the apparent magnitude gives the distance modulus and hence the distance. See also distance determination.

Collins Dictionary of Astronomy © Market House Books Ltd, 2006

Parallax

(pop culture)

In a controversial move during the mid-1990s, DC Comics transformed one of its most famous superheroes—Hal Jordan, aka Green Lantern II— into a supervillain. While always a loyal member of the Green Lantern Corps, Jordan had been known to break rank if his personal beliefs conflicted with the tenets of the Corps' governing body, the Guardians of the Universe. When despots Mongul and the Cyborg Superman destroyed Jordan's hometown of Coast City and exterminated its population of millions, the distraught Green Lantern implored the Guardians to use the Corps' energy source, the Central Power Battery, to restore the city and the lives of its deceased. Forbidden by his keepers to alter history, the maddened Jordan arrogantly waged war against the Corps and destroyed the group, killing or scattering its members. Usurping their power rings and the emerald energy of the Central Power Battery, Jordan transformed himself into the megalomaniacal Parallax in Green Lantern vol. 3 #50 (1994). This move shocked fans and angered many long-time readers who complained that “fearless” and “honest” Hal Jordan—chosen as Earth's most “deserving” candidate to succeed dying Green Lantern Abin Sur in Showcase #22 (1959)—would never stoop to such a heinous act. Partnering with the temporal-villain Extant in the crossover Zero Hour: Crisis in Time (1994), Parallax attempted to reconfigure Earth's timeline under his distorted vision of virtue, but was bested by a conclave of heroes. Parallax also teamed with Marvel Comics' Thanos in the DC/Marvel crossover Green Lantern/Silver Surfer (1995). Redemption came for Jordan when Parallax valiantly sacrificed himself to stop the stellardevouring Sun Eater in the miniseries The Final Night (1996), living on in the afterlife as the Spirit of Vengeance, the Spectre. Jordan returned from the dead and resumed his Green Lantern career in the miniseries Green Lantern: Rebirth (2004–2005). His transformation into villainy was attributed to his possession by an actual creature called Parallax, a malevolent “cosmic parasite” that influenced his behavior. DC Direct produced an action figure of fallen hero Parallax in 2005.

parallax

[′par·ə‚laks]

(optics)

The change in the apparent relative orientations of objects when viewed from different positions.

parallax

The black and white posts are in one line as viewed by an aircraft in the center. The black post appears to the left of the white post when the observer sees it from position A. The observer sees the white post to the left of the black post when the same is viewed from the position B. This is due to parallax.

Parallax.

i. As it relates to photo interpretation, the apparent displacement of the position of a body with respect to a reference point or system caused by a shift in the point of observation. In the illustration, A will see the black post to the right of the white post; the camera at B will see the black post to the left of the white post.
ii. The difference in the direction of a celestial object as seen by an observer from two widely separated points. The measurement of parallax is used directly to find the distance of the body from the earth and from the sun.
iii. The phenomenon in radar imagery when a tall object is imaged and the top of the object is nearer the aircraft. In this case, the slant range to the top of the object is less than that to the base. The object appears to lie toward the aircraft flight path. This is known as radar parallax.

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Parallax

the apparent change in the relative position of an object as a result of movement of the observer’s eye. Parallax can cause errors in the reading of a scale that is not in direct contact with an object whose length is being measured or whose position

Figure 1

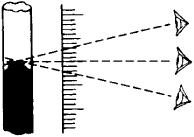
is being determined (see Figure 1). In optical instruments, such as telescopes or microscopes, parallax results from the observer’s eye movement in front of the eyepiece when the graticule or cross hair used for measurement is not in the same plane as the image produced by the objective. The concept of parallax plays an important role in astronomy.

Parallax

in astronomy, the apparent displacement of bodies on the celestial sphere as a result of the movement of the observer in space. The earth’s rotation about its axis is the cause of diurnal parallax, the earth’s revolution about the sun is responsible for annual parallax, and the solar system’s motion in the Galaxy causes secular parallax. Given accurate measurements of the parallactic shifts of celestial bodies or groups of bodies, the bodies’ distances can be determined.

Diurnal parallax. The diurnal parallax of a celestial body is the angle whose vertex is at the center of the body and whose sides are directed toward the earth’s center and the observer’s location on the earth’s surface. The magnitude of the diurnal parallax depends on the zenith distance of the celestial body and varies with a period of 24 hours. The parallax of a body located on the horizon of the observer is called the horizontal parallax; if the observer is on the equator, the horizontal parallax is referred to as the equatorial horizontal parallax and is constant for bodies located at a constant distance from the earth. The relation between the equatorial horizontal parallax p₀ of a celestial body and the body’s geocentric distance r is given by the formula

where R is the radius of the earth’s equator. The distance to the sun, moon, or other bodies within the solar system can be expressed in terms of the body’s equatorial horizontal parallax. Thus, the value 8.79” is taken for the mean distance to the sun, and 57’ 2.6” is taken for the mean distance to the moon. Because the stars are very distant from the earth, diurnal parallax has practically no effect on their positions.

Annual parallax. The annual parallax of a celestial body is the small angle in the right triangle whose hypotenuse is the distance from the sun to the star and whose small leg is the semimajor axis of the earth’s orbit. Annual parallax can be used to determine the distances to stars. Because they are very small, these parallaxes can be regarded as inversely proportional to the distances to the stars; a parallax of 1 “corresponds to a distance of one parsec. The parallax of the nearest star, Proxima Centauri, is 0.76”. Parallaxes determined from the direct measurement of the apparent displacements of stars against a background of considerably more distant stars are called trigonometric. Because of their small value, trigonometric parallaxes have been successfully measured for only the nearest stars. The comparison, however, of the stars’ absolute magnitudes, which can be computed from the stars’ parallaxes, with certain properties of the stars’ spectra has permitted the discovery of relationships that can be used to estimate the distances to other, more remote stars, for which trigonometric parallaxes cannot be determined. Parallaxes computed in this way are called spectroscopic parallaxes.

Secular parallax. The secular parallax of a star is the star’s angular displacement in a year as a result of the motion of the solar system; the displacement is relative to a direction perpendicular to this motion. In contrast to diurnal and annual parallaxes, which are connected with periodic shifts of stars on the celestial sphere, secular parallax is determined by a parallactic shift that increases continuously over time. Because of the proper motions of the stars, secular parallaxes can be determined only statistically, that is, with respect to a sufficiently large group of stars; the peculiar motions of the stars in the group are assumed to average zero. Secular parallaxes are made use of in stellar astronomy, since they permit the estimation of distances that are considerably larger than the distances that can be obtained by measurements of annual parallaxes. The distances corresponding to secular parallaxes, however, are only averages that hold for the entire group of stars involved in the measurements; the distances may differ considerably from the actual distances for individual stars.

REFERENCE

Parenago, P. P. Kurs zvezdnoi astronomii [3rd ed.]. Moscow, 1954.

N. P. ERPYLEV