baryon
Baryon
The generic name for any hadronic particle with baryon number B = +1. By far the most common baryons are the proton and neutron, the two states of the nucleon doublet N = (p, n) [Table 1]. The baryon number of any particular state may be deduced from its production or decay processes, or both, since the total baryon number is conserved (with possible rare exceptions discussed below) and B = 0 holds for all mesons and leptons. See Lepton, Meson, Neutron, Nucleon, Proton
| Flavors | |||||||
|---|---|---|---|---|---|---|---|
| Baryon | Mass, MeV | Spin parity | Strangeness (s) | Charm(c) | Lifetime, s | Dominant decay modes | Magnetic moment, n.m.* |
| p | 938.27200 ± 0.00004 | + | 0 | 0 | >1039 | — | 2.792847 |
| n | 939.56533 ± 0.00004 | + | 0 | 0 | 886 ± 1 | p&ngr;ee- | -1.91304 |
| &Lgr; | 1115.683 ± 0.006 | + | -1 | 0 | 2.63 ± 0.02 × 10-10 | p&pgr;- (64%) n&pgr;0(36%) p&ngr;ee-(0.083 ± 0.002)% | -0.613 ± 0.004 |
| &Sgr;+ | 1189.37 ± 0.07 | + | -1 | 0 | 8.02 ± 0.03 × 10-11 | p&pgr;0 (52%) n&pgr;+(48%) (0.123 ± 0.005)% pγ | 2.46 ± 0.01 |
| &Sgr;0 | 1192.64 ± 0.03 | + | -1 | 0 | 7.4 ± 0.7 × 10-20 | &Lgr;γ | |
| &Sgr;- | 1197.449 ± 0.030 | + | -1 | 0 | 1.48 ± 0.01 × 10-10 | n&pgr;- n&ngr;ee- (0.102 ± 0.003)% | -1.16 ± 0.03 |
| &Xgr;0 | 1314.8 ± 0.2 | + | -2 | 0 | 2.9 ± 0.1 × 10-10 | &Lgr;&pgr;0 | -1.25 ± 0.02 |
| &Xgr;- | 1321.31 ± 0.13 | + | -2 | 0 | 1.64 ± 0.02 × 10-10 | &Lgr;&pgr;- | -0.651 ± 0.003 |
| &Lgr;&ngr;ee- (0.056 ± 0.003)% | |||||||
| &OHgr;- | 1672.4 ± 0.3 | (+?) | -3 | 0 | 0.82 ± 0.01 × 10-10 | &Lgr;K (68%) &Xgr;0&pgr;-(24%) &Xgr;-&pgr;0 (9%) | -2.02 ± 0.05 |
| &Lgr;c+ | 2284.9 ± 0.6 | (+?) | 0 | 1 | 2.0 ± 0.1 × 10-13 | pK-&pgr;+ (5 ± 1)% | — |
| &Sgr;c† | 2452 ± 1 | (+?) | 0 | 1 | hadronic | &Lgr;c+&pgr; (+, 0, -) | — |
| &Xgr;c+ | 2466 ± 2 | (+?) | -1 | 1 | 4.4 ± 0.3 × 10-13 | &Xgr;-&pgr;+&pgr;-, &Lgr;K-&pgr;+&pgr;+ | — |
| &Xgr;c0 | 2472 ± 2 | (+?) | -1 | 1 | 0.1 ± 0.2 × 10-13 | &Xgr;-&pgr;+, &Xgr;-&pgr;+&pgr;+&pgr;- | — |
| &OHgr;c0 | 2698 ± 3 | (+?) | -2 | 1 | 0.6 ± 0.2 × 10-13 | &Xgr;-K-&pgr;+&pgr;- | — |
| &Lgr;b0 | 5624 ± 9 | (+?) | 0 | 0 | 1.23 ± 0.08 ×-12 | &Lgr;c+&pgr;- | — |
| b= -1 | |||||||
| *The abbreviation n.m. denotes the unit eℏ/2Mpc (nuclear magneton). †&Sgr;c is included here, although hadronically unstable, because &Lgr;c, &Sgr;c, &Xgr;c, and &OHgr;c belong to a common SU(3)f multiplet see Fig. 2a. |
It is now generally accepted that hadrons are composite, consisting of spin-1/2 quarks (q), corresponding antiquarks (q), and some number of gluons, the last being the quanta of the intermediate field which binds the quarks and antiquarks to form hadrons. B = + holds for a quark q, B = - for an antiquark q, while B = 0 holds for a gluon. Thus, a baryon consists of three (“valence”) quarks, together with some number of quark-antiquark (qq) pairs (called the quark-antiquark sea) and of gluons. The quarks must be assigned fractional charge values, relative to the proton charge (Table 2). See Gluons, Hadron, Quarks
Color and quantum chromodynamics
This quark theory of the hadrons has been proposed in a quite specific form, known as quantum chromodynamics (QCD). It is a gauge theory based on a symmetry hypothesized for the hadronic interactions of the quarks, which says that these interactions are invariant with respect to a local (gauge) group of unitary transformations with modulus unity, SU(3)C, acting in an abstract complex three-dimensional space known as color space. Each quark type then has three color states, usually labeled by the suffixes r (red), g (green), and b (blue), corresponding to the three axes of this space. The gauge particle of this symmetry theory is the gluon, a neutral vector particle coupled universally with the currents of color, just as the photon, the gauge particle of quantum electrodynamics (QED), is coupled universally with the electromagnetic current. However, whereas the photon has no charge, the gluon has eight color components, so that it is a color octet. Consequently, there is a gluon contribution to the color currents, and so the gluon field must interact with itself, introducing a nonlinearity into quantum chromodynamics which has no parallel in quantum electrodynamics. This nonlinearity has important implications for quantum chromodynamics, leading to its asymptotic freedom, the property that the coupling of gluon to the color current approaches zero at short distances, which is essential for even qualitative agreement between quantum chromodynamics predictions and the empirical data on high-energy collision processes. See Color (quantum mechanics), Quantum chromodynamics, Quantum electrodynamics, Symmetry laws (physics)
| Quark | ||||||
|---|---|---|---|---|---|---|
| type | d (down) | u (up) | s (strange) | c (charmed) | b (bottom) | t (top) |
| Charge | - | - | - | |||
| (Q/ep) | ||||||
| Mass, | ≃0.3 | ≃0.3 | ≃0.5 | ≃1.5 | ≃4.7 | ≃174 |
| GeV† | ||||||
| Flavor | I3 = - | I3 = + | s = -1 | c = +1 | b = -1 | t = +1 |
| Lepton | &ngr;e | e+ | μ+ | &ngr;μ | &tgr;+ | &ngr;&tgr; |
| type | ||||||
| *To each quark and lepton, there exists an antiquark and antilepton with opposite flavor values and with opposite intrinsic parity. †Quark masses are rough estimates of the “effective mass” of each quark in a hadron. |
An important element in quantum chromodynamics is the confinement dogma, the assertion that only color singlet states have finite energy. This assertion implies that neither a quark nor a gluon can exist in a free state, since the former is a color triplet and the latter a color octet, and indeed no observations of free gluons or quarks have yet been confirmed. However, no rigorous proof that the dogma follows from quantum chromodynamics has yet been given.
Quantitative predictions of the properties of baryonic states are currently made by using a simplified quark-quark (q-q) potential with the following features: (1) an attractive long-range potential, increasing with separation to ensure confinement, and (2) a spin-dependent potential representing one-gluon exchange, effective at small separation, where the regime of asymptotic freedom holds and perturbation theory is valid. Such predictions have had a great deal of success.
The quark content of the nucleons is given by Eqs. (1). (1) 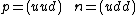
The replacement of a d quark in the nucleon by an s quark produces a baryon state with spin parity + and strangeness number s = -1, the latter being given by [n(s) - n(s)], where n(q) denotes the number of quarks of type q in the system considered. The states thus reached have the flavor structures of Eqs. (2), the other factors
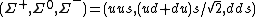
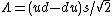
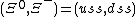
These eight baryon states (p, n, &Sgr;+, &Sgr;0, &Sgr;-, &Lgr;, &Xgr;0, &Xgr;-) all have the spin parity + and the same internal wave functions. It is helpful to use the quantum number Y = (B + s), named hypercharge. Then, if the states are arrayed in the I3 - Y plane (Fig. 1), the symmetry of their relationship is evident.
The mass difference δm = [m(s) - m(u, d)] is quite large, and so SU(3)f symmetry is much more strongly violated than SU(2)&tgr; symmetry. The baryon mass values vary widely over the octet; the leading variation is that proportional to the strangeness s, which counts the s-quark content of each baryon. The approximately 75-MeV difference between the mean &Sgr; mass m(&Sgr;) and m(&Lgr;) has a more subtle origin, but is well accounted for on the basis of the quark-quark (qq) potential from quantum chromodynamics, described above. The small mass differences within each isospin multiplet are believed to be due to the intrinsic (u, d) mass difference and to electromagnetic effects.
The baryon-baryon interactions are of particular interest. That between nucleons gives rise to the existence of atomic nuclei, and has been particularly well studied, both empirically and theoretically. For large separations (greater than 0.8 femtometer), the NN force is due to the exchange of pions and of other known mesons with masses less than about 1 GeV; for small separations (less than 0.4 fm), a strong short-range repulsion is observed, possibly arising from the suppressive effects of the Pauli principle for quarks when the quark structures of the two nucleons overlap. At low energies, the outstanding feature of the NN interaction is its strong noncentral tensor component, which is due to one-pion exchange and is a direct consequence of the pseudoscalar nature of the pion. It also has a strong spin-orbit interaction, observed in NN interactions at higher energy and of much importance for the shell structure of nuclei. See Nuclear structure
Many further particle-unstable baryon states, with lifetimes in the range 10-22 to 10-23 s, have become established, up to mass values of order 2500 MeV, all consistent with the limitations of the three-quark model.
Further baryon states can be formed by replacing one or more of the u, d, and s quarks of the states discussed above by a c quark. If the s and c quarks both had the same mass as the (u, d) quarks, the states formed would correspond to an SU(4)f symmetry. Extensions of the + baryon octet (Fig. 2a) and the + baryon decuplet (Fig. 2b) to arrays in three dimensions are obtained in this way. The lowest plane of each such array consists of the charmless baryon states, in accord with the original octet or decuplet. In reality, the c-quark mass is so large that little quantitative detail of SU(4)f symmetry can survive in the physical situation, and these arrays have value mainly for general comprehension and for the counting of states.
The fifth quark, named “bottom” (symbol b), was discovered in 1978. The baryon &Lgr;b0 is well established, with decay mode &pgr;-&Lgr;c+ and mass 5624 ± 9 MeV. See Upsilon particles
The sixth quark, named “top” (symbol t), became established in 1994 through top-antitop pair production in proton-antiproton collisions at center-of-mass energy 1800 GeV. Its mass, 174 ± 5 GeV, is remarkably large, far above the bW+ threshold at ≈85 GeV. The decay t → bW+ is very rapid, its lifetime being 4 × 10-25 s and its decay width &Ggr;t ≈ 1.5 GeV. This decay is so much faster than hadronization that there is almost no time for top baryons to form.
No further quark-lepton families are expected. This conclusion comes from counting the number of neutrino species in Z0 decays, and from astrophysical arguments about light-nucleus formation in the early universe.
For every baryonic state mentioned above, there will exist an antibaryon state with opposite flavor quantum numbers, in particular with B = -1. The antiproton p was first identified in 1954, and antiproton beams at high-energy proton accelerators are a basic tool in elementary particle research. Most of the expected antibaryon states have been detected and studied in some detail.
In grand unification theories (GUT), which attempt to account for both quarks and leptons, together with their strong, electromagnetic, and weak interactions, quark → lepton transitions generally exist, at some level, since such theories assign leptons and quarks to common multiplets. This violation of baryon conservation opens the possibility that the lightest baryon, the proton, might not be absolutely stable but may undergo decay processes such as p → e+ &pgr;0 at a very low rate. Indeed, cosmology appears to require the existence of nucleon decay processes in order to account for the baryon-antibaryon asymmetry of the universe. Empirically, the partial decay rate &Ggr;(p → e+&pgr;0) is less than 0.58 × 10-40 s-1 with 90% probability. In the simplest GUT [known as SU(5)], this leads to a proton lifetime greater than 1.7 × 1032 years. Other GUTs may predict smaller decay rates, even zero. Since proton decay offers the possibility of discriminating between various GUTs, the detection of proton decay (and neutron decay involving baryon nonconservation, for example, when bound in a deuteron or alpha particle), or at least the improvement of the present empirical limits on its rate, is an important subject of investigation. See Elementary particle, Fundamental interactions, Grand unification theories

