cone

cone

1. Maths

a. a geometric solid consisting of a plane base bounded by a closed curve, often a circle or an ellipse, every point of which is joined to a fixed point, the vertex, lying outside the plane of the base. A right circular cone has a vertex perpendicularly above or below the centre of a circular base. Volume of a cone: ⅓πr²h, where r is the radius of the base and h is the height of the cone

b. a geometric surface formed by a line rotating about the vertex and connecting the peripheries of two closed plane bases, usually circular or elliptical, above and below the vertex

2. Botany

a. the reproductive body of conifers and related plants, made up of overlapping scales, esp the mature female cone, whose scales each bear a seed

b. a similar structure in horsetails, club mosses, etc.

3. a small cone-shaped bollard used as a temporary traffic marker on roads

4. Anatomy any one of the cone-shaped cells in the retina of the eye, sensitive to colour and bright light

Collins Discovery Encyclopedia, 1st edition © HarperCollins Publishers 2005

cone

[kōn]

(botany)

The ovulate or staminate strobilus of a gymnosperm.

(engineering acoustics)

The cone-shaped paper or fiber diaphragm of a loudspeaker.

(geology)

A mountain, hill, or other landform having relatively steep slopes and a pointed top.

(histology)

A photoceptor of the vertebrate retina that responds differentially to light across the visible spectrum, providing both color vision and visual acuity in bright light.

(mathematics)

A solid bounded by a region enclosed in a closed curve on a plane and a surface formed by the segments joining each point of the closed curve to a point which is not in the plane.

(metallurgy)

The part of an oxygen gas flame adjacent to the orifice of the tip.

(textiles)

A bobbin on which yarn is wound for weaving.

McGraw-Hill Dictionary of Scientific & Technical Terms, 6E, Copyright © 2003 by The McGraw-Hill Companies, Inc.

wind cone

Wind cone.

A free-rotating fabric-truncated cone that when subjected to air movement indicates wind direction and wind force. On approach charts, the wind cone is shown as. Also called a cone, sock, or wind sock.

An Illustrated Dictionary of Aviation Copyright © 2005 by The McGraw-Hill Companies, Inc. All rights reserved

The following article is from The Great Soviet Encyclopedia (1979). It might be outdated or ideologically biased.

Cone

 

(mathematics). (1) A cone, or conical surface, is the locus of lines (generators) in space that join all the points of a curve (directrix) to a given point (vertex) in space. If the directrix is a line, then the cone reduces to a plane. If the directrix is a curve

Figure 1

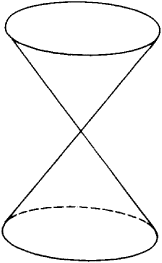
of the second degree not lying in the same plane as the vertex, then we obtain a quadric conical surface (see Figure 1, where the directrix is an ellipse). The simplest surface of this type is a circular, or right circular, cone, whose directrix is a circle and whose vertex can be orthogonally projected to the center of the circle.

Figure 2

Figure 3

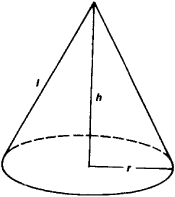
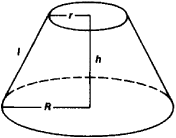
(2) In elementary geometry, a circular cone is a geometric solid bounded by the surface of a circular cone and the plane containing the directing circle (Figure 2). Its volume is equal to πr²h/3, and its lateral area to πrl If a cone is cut by a second plane parallel to the first, a frustum of the cone (Figure 3) is obtained, whose volume is equal to π(R² + r² + Rr)h/3 and whose lateral area is π(R + r)l.

The Great Soviet Encyclopedia, 3rd Edition (1970-1979). © 2010 The Gale Group, Inc. All rights reserved.