mass
Mass
Mass
The quantitative or numerical measure of a body's inertia, that is, of its resistance to being accelerated.
Because it is often necessary to compare masses of such dissimilar bodies as a sample of sugar, a sample of air, an electron, and the Moon, it is necessary to define mass in terms of a property that not only is inherent and permanent but is also universal in that it is possessed by all known forms of matter. All matter possesses two properties, gravitation and inertia. The property of gravitation is that every material body attracts every other material body. The property of inertia is that every material body resists any attempt to change its motion. A body's motion is said to change if the body is accelerated, that is, if it increases or decreases its speed or changes the direction of its motion. Because of its inertia a body cannot be accelerated unless a force is exerted on it. The greater the inertia of a body, the less will be the acceleration produced by a given force. See Gravitation, Inertia
The present definition of mass is in terms of inertia. The masses of two bodies are compared by applying equal forces to the bodies and measuring their accelerations. For example, the two bodies may be allowed to collide. According to Newton's third law, each body will then experience an equally strong force. If there are no external forces, and if a1 and a2 are the measured accelerations of the two bodies, the ratio of the masses of the two bodies is by definition given by the equation
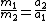
This equation gives only ratios of masses; it is therefore necessary to designate the mass of some one body as the standard mass to which the masses of all other bodies can be compared. The body that has been chosen for this purpose is a cylinder of platinum-iridium alloy. It is known as the international standard of mass; its mass is called 1 kilogram (kg), and it is kept at the International Bureau of Weights and Measures near Paris, France. Replicas of the standard mass, kept at various national laboratories, are periodically compared with this standard.
Einstein's special theory of relativity predicts that the inertia of a body should increase if the energy of the body increases. This prediction has been conclusively verified experimentally. It follows that the mass of a body will increase if, for example, the body gains speed (addition of kinetic energy), or its temperature rises (addition of heat energy), or the body is compressed (addition of elastic energy). See Conservation of mass
mass
A measure of the quantity of matter in a body. The SI unit of mass is the kilogram. The astronomical unit of mass is the solar mass, i.e. 2 × 1030 kg. Mass is a property of matter that determines both the inertia of an object, i.e. its resistance to any change in its motion or state of rest, and the gravitational field that it can produce. The former is called inertial mass, defined by Newton's laws of motion, and the latter is gravitational mass. Inertial and gravitational mass have been found to be equivalent. This led to Einstein's principle of equivalence between inertial and gravitational forces. See also relativity, special theory; stellar mass; weight.mass
see MASS SOCIETY, ÉLITE THEORY.Eucharist
Three of the four Gospel accounts of Jesus' death state that on the night before he died he shared a ceremonial meal with his followers. Christians call this meal the Last Supper and honor it with religious observances that take place on Maundy Thursday. This meal is also commemorated each Sunday in churches throughout the world in a ceremony called the Eucharist. The Eucharist serves as the central and most important ritual in Christian communal worship. As this ceremony recalls the events surrounding Jesus' death and resurrection, it may be thought of as an Easter symbol and custom which millions of Christians participate in every Sunday.
The Last Supper and Passover
Jesus himself founded the ceremony of the Eucharist at the Last Supper (for more on the Last Supper, see Maundy Thursday). Christian scripture asserts that at this meal Jesus gave thanks to God for bread and wine, identified them as his body and blood, and passed them to his disciples to eat and drink (Matthew 26:26-29, Mark 14:22-25, Luke 22:16-19). These words and actions form the basis of the contemporary celebration of the Eucharist. A closer examination of their historical and cultural context illuminates their significance to Jesus'followers and to the first Christians.
The Gospels of Mark, Matthew, and Luke assert that the Last Supper was a Passover meal. (The Gospel according to John implies that the Passover supper would take place on the evening of the following day.) The yearly Passover festival originated in biblical times as a means for Jews to express their gratitude to God for leading their ancestors out of slavery in Egypt over a thousand years before Christ was born (see also Salvation). Through participation in the religious ceremonies associated with Passover, Jews also reaffirmed their relationship with God.
The Book of Exodus tells that the Jews enslaved in Egypt sacrificed a lamb to God and smeared its blood over their doorways as a sign of their faithfulness to the Lord. Afterwards they consumed the sanctified flesh of the lamb, waiting in readiness for God to deliver them.
In Jesus' time religious custom required those celebrating Passover to make a pilgrimage to Jerusalem. Once there they brought a lamb to the Temple, where the animal was killed as an offering to God. The sacrificial lamb recalled the original offering their ancestors made while slaves in Egypt. In Jesus' day worshipers took the lamb home after it had been offered to God by the Temple priests. Then it was roasted and eaten by a gathering of family and friends. This ceremonial meal also included unleavened bread and wine.
Scriptural accounts of the Last Supper describe a meal that resembles a traditional Passover supper in some ways and diverges from Jewish custom in others. As in a traditional Jewish Passover meal, Jesus gave thanks to God for the bread and wine before passing them to his disciples. But in a sharp break from Jewish religious teaching he proclaimed that the bread was his body and the wine his blood. In Matthew's account Jesus adds that his blood is "my blood of the covenant, which is poured out for many for the forgiveness of sins" (Matthew 26:28). Here Jesus is painting himself as a new kind of sacrificial lamb, one whose death will rescue his followers from the consequences of sin, and pave the way to a new relationship with God.
Origins of the Eucharist
The first Christians quickly interpreted Jesus' words and deeds at the Last Supper in terms of the Passover themes of sacrifice, redemption, and salvation. Jesus' death on the cross on Good Friday became the sacrifice which reunited a straying humanity with God. By accepting Jesus' body and blood as represented in bread and wine at the Last Supper, Jesus' original followers accepted both his act of sacrifice and the spiritual renewal that sprang from it. The early Christians developed a ceremony called the Eucharist in order that Jesus' growing numbers of followers could also share in this new relationship with God and one another through Christ. Just as religious Jews consumed the flesh of the Passover lamb, the new ceremony required Christians to consume the body and blood of the Savior who had died for their sakes. The body and blood were represented, as they had been at the Last Supper, by bread and wine.
The word "Eucharist" is an English pronunciation of the ancient Greek word eucharistia, which means "thanksgiving" or "gratitude." This name, given to the ceremony by the early Christians, reflects their attitude towards it. The ceremony and the prayers that accompanied it expressed their gratitude to Christ for rescuing them from sin, opening the door to a new relationship with the Divine, and promising them eternal life. At first, groups of Christians shared bread and wine together informally, as part of an everyday meal. As time went by this sharing of bread and wine grew increasingly ceremonial. By the fourth century Christians were celebrating the Eucharist in public buildings under the supervision of robed clergy, accompanied by Bible readings, prayers, chants, homilies, and the prayer of thanksgiving, which retold Jesus'words and deeds at the Last Supper.
Interpreting the Eucharist
Over the centuries many controversies have erupted over differing interpretations of the Eucharist. One of the most significant debates took place during the sixteenth-century western European Reformation. This period of religious strife gave birth to Protestant Christianity. Among other things, Protestants disagreed with the Roman Catholic doctrine concerning the Eucharist. This doctrine states that although neither the bread nor the wine of the Eucharist seems to change in appearance, they change in actual substance, becoming the real body and blood of Christ. Roman Catholic theologians explained the mechanics of this transformation in a doctrine known as transubstantiation. Protestant reformers disagreed with the idea that the bread and wine change into the actual body and blood of Christ. Today's many Protestant denominations attribute varying shades of meaning to the ceremony, but most tend to view the bread and wine as symbols that represent the body and blood of the Savior. They would also affirm, however, that Christ, through the power of the Holy Spirit, is indeed present with those who participate in the ceremony.
Other differences distinguish Protestant and Roman Catholic views of the Eucharist. Whereas Roman Catholic theology views the ceremony as an invitation to worshipers to partake of Jesus'sacrifice, many Protestant theologians instead see it as a memorial, or reminder, of Jesus' sacrifice.
The Orthodox Christians of eastern Europe, the Middle East, and north Africa offer yet another perspective on the ceremony. Like Roman Catholics they tend to view the ceremony as Jesus' renewed offering of himself to the assembled worshipers. They also agree that worshipers partake of the actual body and blood of Christ. Yet unlike Roman Catholic theologians, Orthodox theologians offer no definite explanation for how this miracle takes place. Instead they view Christ's presence in the bread and wine of the Eucharist as a mystery. By "mystery" they mean one of the hidden and unfathomable ways that God works in the world, sometimes perceived by those who look through the eyes of faith. Therefore the best way to "understand" the Eucharist is to participate in it with reverence, prayer, and meditation. In sum, Orthodox Christian authorities approach the ceremony as a spiritual experience to be savored rather than an intellectual problem to be solved.
Contemporary Ceremonies and Services
Today many different versions of the ceremony exist. Nevertheless, the heart of the ritual consists of the identification of bread and wine as Jesus' body and blood and the invitation to worshipers to partake of them. In doing so Christians remember Jesus' sacrificial death and resurrection and commit themselves again to the new covenant, or relationship with God, that these events brought about. They ask to draw nearer to God through Christ, and accept the spiritual healing, or salvation, that comes from this relationship. Participation in the ceremony helps to create a feeling of fellowship between worshipers as they together share in God's hospitality, expressed in spiritual food and drink. At some contemporary Protestant services grape juice substitutes for wine (for more on this issue, see also Wine).
In many churches, including those of the Roman Catholic, Orthodox, and Anglican traditions, the Eucharist stands at the heart of the Sunday worship service. Protestants, in general, celebrate the Eucharist less frequently. In some denominations the ceremony is known as the Eucharist, while in others it may be called the Lord's Supper or Holy Communion. Various Christian denominations have assigned different names to the worship service centered around the celebration of the Eucharist. Roman Catholics and some Anglicans call it a "Mass" and Orthodox Christians know it as the "Divine Liturgy." Protestants refer to the service by a variety of names, including the Eucharist, the Lord's Supper, or Holy Communion.
Further Reading
Ferguson, Everett, ed. "Eucharist." In his Encyclopedia of Early Christianity. Volume 1. New York: Garland, 1997. Hellwig, Monica K. "Eucharist." In Mircea Eliade, ed. The Encyclopedia of Religion. Volume 5. New York: Macmillan, 1987. "Hospitality." In Leland Ryken, James C. Wilhoit, and Tremper Longman III, eds. Dictionary of Biblical Imagery. Downers Grove, IL: InterVarsity Press, 1998. McNicol, Allan J. "Lord's Supper." In David Noel Freedman, ed. Eerdmans Dictionary of the Bible. Grand Rapids, MI: William B. Eerdmans Publishing, 2000. Peifer, C. J. "Passover Lamb" and "Passover Meal." In New Catholic Ency- clopedia. Volume 10. New York: McGraw-Hill, 1967. "Redemption." In Leland Ryken, James C. Wilhoit, and Tremper Longman III, eds. Dictionary of Biblical Imagery. Downers Grove, IL: InterVarsity Press, 1998. Reumann, John. The Supper of the Lord. Philadelphia, PA: Fortress Press, 1985. "Supper." In Leland Ryken, James C. Wilhoit, and Tremper Longman III, eds. Dictionary of Biblical Imagery. Downers Grove, IL: InterVarsity Press, 1998. Williams, Sam K. "The Lord's Supper." In Paul J. Achtemeier, ed. The Harper- Collins Bible Dictionary. New York: HarperCollins, 1996.
Web Sites
An explanation of the Orthodox understanding of the Eucharist, posted by the Orthodox Church in America web site: chri/Orthodox-Faith/Worship/Holy-Eucharist.html
An article entitled "The Holy Eucharist," by the Rev. Thomas Fitzgerald, posted at the Greek Orthodox Archdiocese of America in New York, NY, web site:
mass
[mas]Mass
a physical quantity; a fundamental characteristic of matter that defines its inertial and gravitational properties. A corresponding distinction is made between inertial and gravitational mass.
The concept of mass was introduced in mechanics by I. Newton. In Newtonian classical mechanics, mass is part of the definition of the momentum of a body: the momentum P is proportional to the velocity of motion v of the body,
(1) p = mv
The proportionality factor—the quantity m, which is constant for a given body—is the mass of the body. An equivalent definition of mass can be obtained from the equation of motion of classical mechanics:
(2) f = ma
Here the mass is the proportionality factor between the force f acting on a body and the acceleration of the body a that it causes. The mass defined by equations (1) and (2) is called the inertial mass, or inert mass; it characterizes the dynamic properties of a body and is a measure of the body’s inertia. The greater the mass of a body, the smaller the acceleration it acquires upon application of a constant force—that is, the more slowly its state of motion changes (the greater its inertia).
The mass ratio of various bodies may be determined by applying a given force to them and measuring their acceleration: m1 : m2 : m3,… = a1 : a2 : a3.… If one of the masses is taken as the unit of measurement, then the masses of the other bodies can be found.
In the Newtonian theory of gravitation, mass assumes a different form—it is the source of the gravitational field. Each body creates a gravitational field proportional to its mass and experiences the effect of the gravitational field generated by other bodies, whose force is also proportional to the masses of the bodies. This field causes the attraction of any other body to the given body with a force that is defined by Newton’s law of gravitation:
![]()
where r is the distance between the bodies, G is the universal constant of gravitation, and m1 and m2 are the masses of the attracting bodies. A formula for the weight P of a body of mass m in the earth’s gravitational field may be easily obtained from formula (3):
(4) P = m · g
Here g = G·M/r2 is the free-fall acceleration in the earth’s gravitational field and r ≈ R is the radius of the earth. The mass defined by equations (3) and (4) is called the gravitational mass of the body.
In principle it does not follow that a mass that creates a gravitational field also defines the inertia of the same body. However, experiment has shown that inertial and gravitational mass are proportional to each other (and, with the choice of ordinary units of measurement, are numerically equal). This fundamental natural law is called the principle of equivalence. Its discovery is associated with Galileo, who established that all bodies on earth fall with identical acceleration. Einstein, who was the first to formulate this principle, made it the basis for the general theory of relativity. The principle of equivalence has been established experimentally with very high accuracy. A precise test of the equality of inertial and gravitational masses was first made (1890-1906) by L. Eötvös, who found that the masses coincide with an error of ˜ 10’8. The error was reduced to 10-11 by the American physicists R. Dicke, R. Krotkov, and P. Roll in 1959-64 and to 10-12 by the Soviet physicists V. B. Braginskii and V. I. Panov in 1971.
The principle of equivalence makes possible the most natural determination of the mass of a body, by weighing.
Mass was originally considered (by Newton, for example) to be a measure of the quantity of matter. This definition has clear meaning only for comparison of homogeneous bodies that are constructed of the same material. It emphasizes the additivity of mass—the mass of a body is equal to the sum of the mass of its parts. The mass of a homogeneous body is proportional to its volume; therefore, the concept of density—the mass per unit volume of a body—may be introduced.
In classical physics it was believed that the mass of a body does not change in any processes. The law of conservation of mass (matter), which was discovered by M. V. Lomonosov and A. L. Lavoisier, corresponded to this. In particular, the law asserted that in any chemical reaction the sum of the masses of the initial components is equal to the sum of the masses of the final components.
The concept of mass acquired deeper meaning in the mechanics of Einstein’s special theory of relativity, which considers the motion of bodies (or particles) with very great velocity to be comparable to the speed of light, c ≈ 3 × 1010 cm/sec. In the new mechanics, which is called relativistic mechanics, the relation between the momentum and velocity of a particle is given by the equation
![]()
For low velocities (v « c) this equation becomes the Newtonian relation p = mv. Therefore, the quantity mo is called the rest mass, and the mass m of a moving particle is defined as the proportionality factor between p and v, which is dependent on the velocity:
![]()
Keeping in mind this formula in particular, we say that the mass of a particle (body) increases as its velocity. This relativistic increase in the mass of a particle with increased velocity must be taken into account in the design of high-energy particle accelerators. The rest mass m0 (the mass in a frame of reference that is connected with the particle) is the most important intrinsic characteristic of a particle. All elementary particles have strictly defined values of m0 that are inherent in the given type of particle.
It should be noted that in relativistic mechanics the definition of mass from equation of motion (2) is not equivalent to the definition of mass as the proportionality factor between the momentum and velocity of a particle, since its acceleration ceases to be parallel to the force that causes it, and the mass is found to be dependent on the direction of the particle’s velocity.
According to the theory of relativity, the mass m of a particle is related to its energy E by the equation
![]()
The rest mass determines the internal energy of a particle—its rest energy, E0 ×m0c2. Thus, energy is always related to mass (and vice versa). Therefore, the laws of conservation of mass and energy do not exist separately (in contrast to classical physics) but are fused into the unified law of conservation of total energy (that is, including the rest energy of the particles). Its approximate division into the law of conservation of energy and the law of conservation of mass is possible only in classical physics, when the particle velocities are low (v « c) and processes of conversion of particles do not take place.
In relativistic mechanics, mass is not an additive characteristic of a body. When two particles are combined, forming a composite stable state, an energy excess ΔE (equal to the binding energy), which corresponds to the mass Δm = ΔE/c2, is released in the process. Therefore, the mass of a composite particle is less by the quantity ΔE/c2 than the sum of the masses of the particles that form it (the mass defect). This effect is particularly strongly manifested in nuclear reactions. For example, the mass of a deuteron (d) is less than the sum of the mass of a proton (p) and a neutron (n); the mass defect Δm is related to the energy Eγ of the gamma quantum (y) that is produced during the formation of a deuteron: p + n → d + γ, Ey + Δm·c2. The mass defect that arises during the formation of a composite particle reflects the natural relation between mass and energy.
The gram is the unit of mass in the cgs system of units and the kilogram in the International System of Units. The mass of atoms and molecules is usually measured in atomic mass units. The mass of elementary particles is commonly expressed either in units of mass of the electron me or in energy units, by indicating the rest energy of the corresponding particles. For example, the mass of the electron is 0.511 mega electron volt (MeV); the mass of the proton is 1,836.1 me, or 938.2 MeV.
The nature of mass is one of the most important unsolved problems of modern physics. It is commonly assumed that the mass of an elementary particle is determined by the fields associated with it (such as electromagnetic and nuclear fields). However, a quantitative theory of mass has not been developed, nor are there theories that would explain why the masses of elementary particles form a discrete spectrum of values or possible determination of the spectrum.
In astrophysics, the mass of a body that generates a gravitational field determines the gravitational radius of the body, Rg = 2GM/c2. Because of gravitational attraction no radiation, including light, can emerge from the surface of a body having a radius R≦Rg. Stars of such dimensions would be invisible; therefore, they are called black holes. Such celestial bodies should play an important role in the universe.
REFERENCES
Jammer, M. Poniatie massy v klassicheskoi i sovremennoifizike. Moscow, 1967. (Translated from English.)Khaikin, S. E. Fizicheskie osnovy mekhaniki. Moscow, 1963.
Elementarnyi uchebnik fiziki, 7th ed., vol. 1. Edited by G. S. Landsberg. Moscow, 1971.
Mass
the name of the liturgy used by the Catholic Church.
The components and the order of conducting the mass took shape over the course of many centuries. They became essentially fixed at the Council of Trent (1545–63). The Second Vatican Council (1962–65) made changes in the mass (for example, permitting the service to be conducted in local languages as well as in Latin). The liturgical songs forming an invariable part of a given service make up what is called the ordinary of the mass. They are named after the initial word of each text: Kyrie, Gloria, Credo, Sanctus and Benedictus, and Agnus Dei. Originally, the liturgical songs of the mass were monophonic, based on the Gregorian chant. Later, with the development of polyphony, there appeared polyphonic arrangements of the liturgical music of the mass as well as entire ordinaries of the mass written for the traditional text by just one composer. There was also a distinction made between the high mass (missa solemnis) and the low mass (missa brevis), which consisted as a rule of the first two or three liturgical parts of the ordinary of the mass.
In the Renaissance era the mass was the most monumental of musical genres. Masses were written by J. Dunstable (England), G. Dufay, J. Ockeghem, J. Obrecht, Josquin Depres, and O. de Lassus (the Netherlands), Palestrina, A. Willaert, and G. Gabrieli (Italy), and T. L. de Victoria (Spain). At a later period, classical versions of the mass were composed by J. S. Bach (Mass in B minor), Mozart, Beethoven (two masses, including the Missa Solemnis), L. Cherubini, F. Schubert, F. Liszt, and A. Bruckner. The funeral mass is known as a requiem.
REFERENCES
Bobrovnitskii, I. O proiskhozhdenii i sostave rimsko-katolicheskoi liturgii i otlichii ee ot pravoslavnoi, 4th ed. Kiev, 1873.Ivanov-Boretskii, M. V. Ocherk istorii messy. Moscow, 1910.
Wagner, P. Geschichte der Messe. Leipzig, 1913.
B. V. LEVIK