variable
variable
Short for variable star.variable
a characteristic which can be measured and which may vary along a continuum, continuous variable (e.g. height), be more discrete (e.g. family size) or be bipolar (e.g. sex). The term is commonly used in empirical social research to denote the representation of a social factor such as age, social class, employment status, years of education, which can be observed to affect other measures, such as income level (which may be influenced by all of those mentioned). Social and psychological research is particularly interested in defining what aspects of society or experience influence other social parameters or behaviours, with the intention of explaining social phenomena. On one view, for this to be managed scientifically, possible influences and possible effects have to be defined and quantified so that methods such as concomitant variation, survey research or experiment can be set up to test HYPOTHESES. It is these definitions and quantifications that result in the variables which are used in scientific data analysis. It should be noted that continuous variables are measured on an interval scale, while discrete variables often use nominal or ordinal measurement (see CRITERIA AND LEVELS OF MEASUREMENT).In some traditions in sociology, however, the appropriateness of the concept of the variable in the above sense has been questioned. From the perspective of SYMBOLIC INTERACTIONISM, for example, Herbert BLUMER (1956) has suggested that the use of standardized variables in social analysis leads to a neglect of the close study required for the effective study of social situations and a distorted representation of social reality. Similar scepticism is voiced in approaches such as ETHNOMETHODOLOGY (see also MEASUREMENT BY FIAT, OFFICIAL STATISTICS).
variable
[′ver·ē·ə·bəl]variable
(programming)x = y + 1
means "add one to y and store the result in x". This may look like a mathematical equation but the mathematical equality is only true in the program until the value of x or y changes. Furthermore, statements like
x = x + 1
are common. This means "add one to x", which only makes sense as a state changing operation, not as a mathematical equality.
The simplest form of variable corresponds to a single-word of memory or a CPU register and an assignment to a load or store machine code operation.
A variable is usually defined to have a type, which never changes, and which defines the set of values the variable can hold. A type may specify a single ("atomic") value or a collection ("aggregate") of values of the same or different types. A common aggregate type is the array - a set of values, one of which can be selected by supplying a numerical index.
Languages may be untyped, weakly typed, strongly typed, or some combination. Object-oriented programming languages extend this to object types or classes.
A variable's scope is the region of the program source within which it represents a certain thing. Scoping rules are also highly language dependent but most serious languages support both local variables and global variables. Subroutine and function formal arguments are special variables which are set automatically by the language runtime on entry to the subroutine.
In a functional programming language, a variable's value never changes and change of state is handled as recursion over lists of values.
variable
A structure that holds data within an executable program. Mostly created by and uniquely named by the programmer, variables may store predefined data at the start of the program or be empty containers until a value is placed in them. The values may remain constant or be updated in RAM as the program runs. Variables are used as counters to sum totals and do math as well as to keep track of processes that are repeated within the program. There may be dozens or hundreds of variables defined in a single application.Using C/C++ as the example language, the statement int counter; defines an integer variable for whole numbers named COUNTER. The statement counter=1; stores a 1 in COUNTER, and counter++; adds 1 to COUNTER. A "char" variable holds character data. A single character variable requires single quotes, but a "string" of characters uses double quotes; for example, mode='A'; and product="abc"; places A in the variable MODE and ABC in PRODUCT. See string, integer and RAM.
Variables Are Control Values
Variables are widely used to repeat a process. In the following for statement, the function DO-SOMETHING is performed five times. At first, x is set to 0. All statements between the left and right curly braces ({ }) are performed. Then, x is incremented by 1 until x is no longer less than 5.
for (x=0; x<5; x++) { do-something(); }Local and Global Variables
A local variable is one that is referenced only within the subprogram, function or procedure it was defined in. A global variable can be used by the entire program. See environment variable, undefined variable and local variable.
Actual Variable Examples
The following integer variables and character strings were extracted from a program written in C that converts an XML encyclopedia feed to an HTML feed. The =NO is the same as inserting a 0. Variables are often used to keep track of internal modes that are turned on and off while the program is running. YES and NO are the same as 1 and 0 to the compiler.
int ForceOne=NO, ForceAll=NO, NoMoreFiles=NO; int XMLfileNewer=NO, EndFile=NO; int TermsWith1Link=0, TermsWith2Links=0; int TermsWith3Links=0, TermsWithNoLinks=0; int AFTermCount=0; int AF_results=0; int AF_EOF=0; int hFileAF; int ARTICLES=0; char AFbuff[2000]; char *AFptr; char HREF1buff[500]; char HREF2buff[500]; char HREF3buff[500];
Variable
a fundamental concept of mathematics and logic. Beginning with the works of P. de Fermat, R. Descartes, I. Newton, G. W. von Leibniz, and other founders of higher mathematics, a variable was understood as a quantity that can vary—in the process of this variation it takes on different values. Variables were thus contrasted with constants—numbers or other quantities each of which has a unique, completely defined value. As mathematics developed and work proceeded on its foundations, great pains were taken to exclude such concepts as processes and variation of quantities from the vocabulary of mathematics as being extramathematical. The variable consequently came to be interpreted as a symbol for an arbitrary element of the domain of objects under consideration—for example, the domain of natural numbers or of real numbers. In other words, a variable was now seen as a generic name for the entire domain; constants, on the other hand, were proper names for numbers or other specific objects in the domain under consideration.
This revision of the concept of variable was closely connected with the reorganization of mathematics on the foundation of set theory, a process that was completed in the late 19th century. For all the simplicity and naturalness of this reorganization, it was essentially based on the abstraction of actual infinity. This abstraction permitted arbitrary infinite sets to be considered as “given” (“completed,” “ready,” “actual”) objects, to which all the methods of classical logic could be applied without regard for the incompletedness and the fundamental impossibility of completing the process of the formation of such a set. The difficulties in solving the logical problems associated with the adoption of this abstraction make understandable the partial rehabilitation of the old concepts of variable quantities. In constructing mathematical theories, the representatives of some schools, such as mathematical intuitionism and the constructive trend, have preferred to make do with the weaker, but logically less vulnerable, abstraction of potential realizability. This point of view associates infinite sets with the concepts of the processes of the sets’ generation—processes that go as far as desired but never end. When investigating the problem of the consistency of different fields of mathematics, most mathematicians and logicians in effect adopt this position.
In formalized languages (calculi, or formal systems) of mathematical logic, the term “variable” is applied to any symbol of a strictly fixed type that under certain conditions permits an expression of the given calculus to be substituted for it. Such variables are called free variables. An example is the variable x in the inequality x > 5. If, say, the numeral (that is, the symbol of the number) 7 is substituted for x, the inequality becomes a true statement; if the numeral 2 is substituted, the inequality becomes a false statement. What are called bound variables do not mean anything in themselves but perform purely syntactical functions; when certain elementary precautions are observed, bound variables can be “renamed”—that is, they can be replaced by other variables. An example is the variable y in the expressions
![]()
in the interpretations of which y does not appear and can be replaced by any other variable. Thus, the first expression, which can be read “the sum of the integers from 5 through 25,” can be replaced by
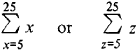
The second expression, which might be read “all numbers have the property p,” can be replaced by ∀tP(t). Individual, proposition, predicate, function, number, and other types of variables are distinguished. They can be replaced, in accordance with special substitution rules, by symbols for, respectively, the objects from the domain under consideration (“terms”), specific statements, predicates, functions, numbers, and so on. Thus, a variable in a formula can be meaningfully understood as an empty place equipped with an indication that the place can be filled—the variable is like a container for a strictly defined piece of merchandise.
Free occurrences of variables in the expressions of meaningful scientific theories and in the formulas of logical and mathematical calculi correspond to the use of indefinite pronouns in ordinary speech and permit of different interpretations. One type of interpretation, which corresponds to the use of a variety of substitution procedures, is the predicate interpretation: the formula A (x1, … xn) of some calculus is interpreted as an n-place predicate. The same formula can also be interpreted as a proposition, or statement, specifically as the proposition ∀x1 … ∀xnA (x1, …, xn), which is a “closure” of the formula—this is the interpretation of universality, which is commonly used, for example, in formulating the axioms of various scientific theories. Finally, to free variables there can be ascribed values constant within some context—for example, the context of a conclusion from a given set of formulas. The variables are then called the parameters of the context, and we speak of the conditional interpretation. For example, the variable x in the expression cos x, taken in isolation, has a predicate interpretation. In the identity sin2x + cos2x = 1 it has the interpretation of universality. In the equation cos x = 1 (in the process of solving this equation, when the variable is called an “unknown”) it has the conditional interpretation.
Thus, at different levels of formalization the concept of the variable acts as a refinement of means commonly used in ordinary spoken languages—such as indefinite pronouns and indefinite articles—and of various methods of employing these means.
REFERENCES
Kleene, S. C. Vvedenie ν metamatematiku, subsecs. 31, 32, 45. Moscow, 1957. (Translated from English.)Church, A. Vvedenie ν matematicheskuiu logiku, vol. 1, subsecs. 02, 04, 06. Moscow, 1960. (Translated from English.)